Inscription / Connexion Nouveau Sujet
Optique : Loi de Snell-Descartes
Bonjour,
ceci est mon premier poste, excusez-moi pour les potentiels erreurs.
J'ai des difficultés pour une partie d'une question de l'exercice suivant : (j'ai mis la partie en question en rouge).
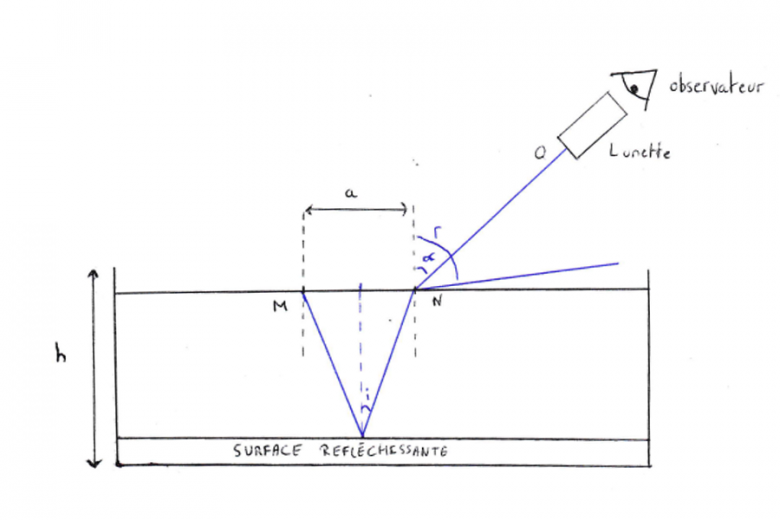
Un récipient dont le fond est réfléchissante contient un liquide d'indice n que l'on souhaite mesurer. Pour cela, deux sources lumineuses M et N supposées ponctuelles sont placées à la surface du liquide. Elles sont séparées d'une distance a supposée parfaitement connue.
Une lunette, située au bord du récipient, permet à un observateur de récolter certains rayons provenant de la surface du liquide. Pour que la lumière puisse pénétrer dans la lunette, nous supposerons que le rayon doit passer par le point O, symbolisant l'entrée de la lunette. La hauteur h du liquide est un paramètre que l'observateur ajuste pour pouvoir déterminer l'indice n. Les sources ponctuelles M et N peuvent envoyer des rayons dans toutes les directions.
B-1) Un observateur, dont l'il est situé derrière la lunette, regarde le point N directement. Sur le schéma représenter le rayon qui va directement de N au point O. Tracer la normale en N. On appelle α l'angle entre la normale en N et ce rayon. Indiquez cet angle sur votre schéma.
B-2-a) Représenter le rayon particulier qui part de M vers le fond du récipient et qui, après réflexion sur le fond, traverse la surface du liquide en N. Soit H le point sur le fond du récipient où est réfléchi ce rayon. Comment est situé le point H par rapport aux point M et N ? Placer ce point sur votre schéma. Représenter le rayon issu de H réfracté en N. On note i l'angle d'incidence en H, r l'angle de réfraction dans l'air en N (pour l'instant, le rayon réfracté en N ne passe pas forcément par O, c'est-à-dire que les angles r et α ne sont pas forcément égaux). Indiquer i et r sur votre schéma.
B-2-b) L'observateur regarde en même temps le point N et l'image du point M après réflexion sur le fond du récipient et traversée de la surface liquide-air. Il ajuste la hauteur h du liquide pour que l'image de M soit vue dans la même direction que le point N. Quelle relation a-t-on lors entre r et α ? Dans ces conditions, écrire la troisième loi de Snell-Descartes pour le rayon provenant du fond de la cuve et réfracté en N Montrer que dans ces conditions, on a n = sinα *
Il y également une question B-2-c) mais elle consiste en une application numérique sans trop de difficultés qui ne m'a pas posé de problème.
Ce que j'ai tenté pour montrer l'égalité :
n*sin(i) = nair *sin(α)
n*sin(i) = sin(α)
Or sin(i) =
donc n =
et la je bloque...
Voici dont il est question dans l'exercice, (la partie noire est la partie originale, et la bleu les parties que j'ai complété au fur et à mesure de l'exercice).
bonsoir
Tu y es presque ! Comme tu l'as écrit :
Sur ta figure, en notant H le point de réflexion sur le fond et O le milieu du segment (MN), le théorème de Pythagore conduit à :
Tel que je comprends l'énoncé, la formule que tu fournis permute h et a. Réfléchissons un peu au sens physique du problème : a et  étant fixés, supposons que n augmente, cela impose une diminution de l'angle i donc une augmentation de h. À a et
étant fixés, supposons que n augmente, cela impose une diminution de l'angle i donc une augmentation de h. À a et  fixés, n est fonction croissante de h.
fixés, n est fonction croissante de h.
Bonsoir, merci pour ta réponse ! Cela m'a un peu éclaircit.
En effet, je n'avais pas vu l'exercice sous cet angle... J'ai cependant réussi à avancer dans mon calcul mais je ne parviens pas à passer de :
à
Concrètement c'est le passage de la première relation à la deuxième qui me pose souci 
Voici ce que j'ai pu faire en reprenant tes notations :
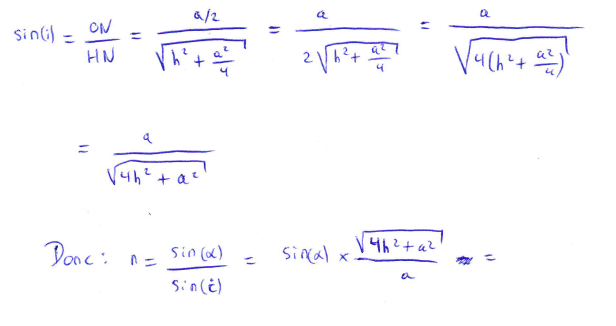
Ton dernier résultat est bon ! Divise maintenant numérateur et dénominateur par a.
un "1" apparaît au dénominateur. Diviser le numérateur par a revient à diviser les termes de la racine carrés par a2. Et tu y es !




