Niveau licence

Optique lentille plan convexe

Posté par
bluq 01-05-17 à 16:37

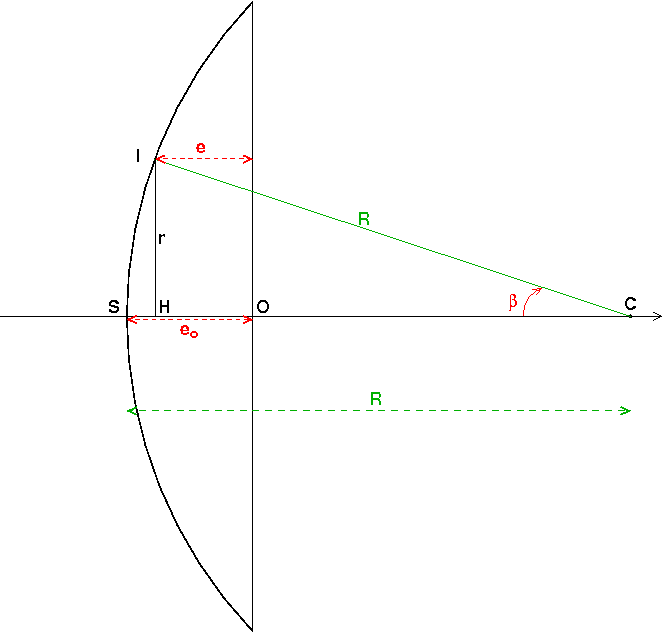
Bonjour , ci dessous mon exercice:

on montre que les chemins (FM) et (FH) sont égaux (Malus), ensuite de cette egalité on déduit e(r)= e₀ - r²/[2(n-1)f']

à partir de là je ne vois pas comment déduire le rayon de la lentille ...

Si quelqu'un se sent l'esprit libre , çà m'aiderait beaucoup qu'il m'explique...

Sur ce, bonne fête du travail à tous!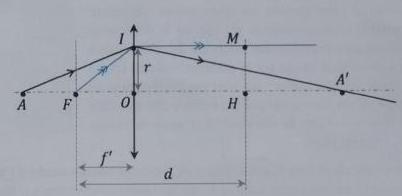

Optique lentille plan convexe

***Image recadrée --> un énoncé est à RECOPIER***

Posté par re : Optique lentille plan convexe 01-05-17 à 16:44

J'ai oublié de préciser qu'on se place en approximation (r très petit), conditions de Gauss

FI=f'+(r²/2f')

Posté par re : Optique lentille plan convexe 01-05-17 à 18:21

Bonjour
Tu ne précises pas le type de lentille : plan - convexe; convexe -plan ; biconvexe. ..

Posté par re : Optique lentille plan convexe 01-05-17 à 22:40

C'est une lentille plan-convexe

Posté par re : Optique lentille plan convexe 02-05-17 à 17:55

Sous réserve que la situation à étudier corresponde bien au schéma ci-dessous... (Ai-je bien « deviné » ?)

$e_{0}-e=SH=SC-HC=R.\left[1-\cos\left(\beta\right)\right]$

Dans les conditions de Gauss : $\beta\ll1rad$ ; $\cos\left(\beta\right)\approx1-\frac{\beta^{2}}{2}$

$e_{0}-e\approx R\frac{\beta^{2}}{2}$

Or :

$\sin\left(\beta\right)=\frac{r}{R}\quad avec\quad\sin\left(\beta\right)\approx\beta$

Finalement :

$e_{0}-e\approx\frac{r^{2}}{2R}$

Optique lentille plan convexe