Inscription / Connexion Nouveau Sujet
Optique : Le chat et le poisson
Bonjours j'ai encore un soucis de compréhension mais en optique cette fois, dont voici l'intitulé :
Un chat et un poisson s'observent mutuellement à travers une la vitre d'un aquarium rectangulaire.
Sachant que la distance réelle entre le chat et la vitre est de 15 cm. n(eau)= 1,33.
La première question me demande de déterminez cette distance telle qu'elle est perçue par le poisson.
Là ou je suis bloquer c'est que si tout les rayons de lumière partent du chat, parallèles, et atteignent avec un angle perpendiculaire la surface de l'aquarium, alors l'angle d'incidence par rapport à la normal à la surface de séparation est nul donc d'après la loi de Snell et Descartes l'angle d'incidence est nul lui et l'angle de réfraction est nul lui aussi par rapport à la normal donc les rayons lumineux continueront tout droit dans l'aquarium donc je ne voit pas comment déterminer la distance que le poisson perçoit, si quelqu'un peut m'aider je l'en remercie d'avance !
Bonsoir
Tu dois revoir ton cours sur le dioptre plan et les formules de conjugaison qui vont avec. Pour mieux comprendre, tu peux imaginer un objet AB parallèle au dioptre et tracer quelques rayons issus de B...
C'est ce que j'ai fait avec un rayon qui part de de B parallèle à l'axe optique mais d'après SnelL et Descartes le rayon ne rejoint pas le foyer F' mais continu tout droit ensuite j'ai tracer un rayon issue de B et passant par 0 dont lui aussi il continu tout droit ensuite si je trace un troisième rayons, je ne voit pas trop comment il se comporte après le passage dans le dioptre
Je pense avoir comprit mais dans le premier car du rappel il est marquer sur le schéma que n1<n2 alors que les rayons réfracter s'éloignent de la normal, je trouvais ça bizarre sinon avec la formule donner je trouve que le poisson perçoit le chat à une distance d=19,95 cm, maintenant j'essaie de comprendre d'ou vient cette formule
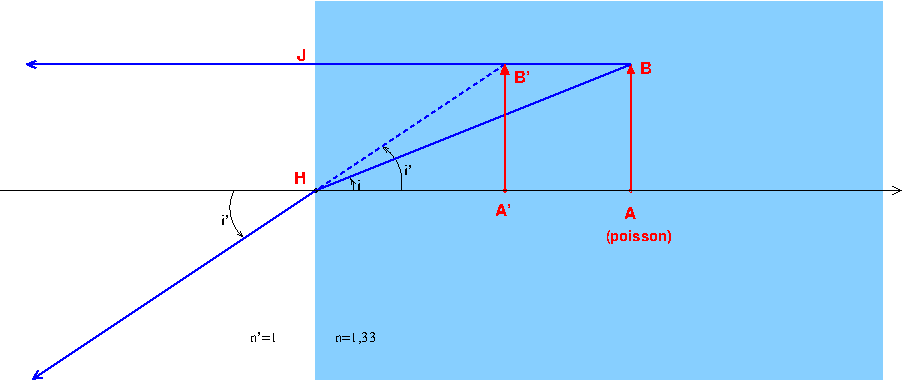
J'ai refais ci-dessous une figure adaptée à la situation du chat qui regarde le poisson, représenté simplement par la flèche AB. Pour plus de clarté, j'ai fortement exagéré les valeurs des angles entre les rayons et les normales au dioptre. Je trace deux rayons issus du point B :
Le rayon BJ confondu avec une normale au dioptre donc non dévié par la réfraction en J. Le rayon passant par H qui lui subit une déviation par réfraction.
n.sin(i)=n'.sin(i') ; puisque n>n' : sin(i)<sin(i') ; comme la fonction sinus est monotone croissante entre 0° et 90°, cela conduit à i<i'.
L'il du chat placé dans l'air à gauche de la figure, reçoit des rayons dont les prolongements passes par B'. B' est ainsi l'image virtuelle de B. Puisque les angles i et i' sont supposés très faibles : sin(i) tan(i) et sin(i')
tan(i) et sin(i') tan(i')
tan(i')
Cela permet de retrouver les formules de conjugaisons du document.
D'accord j'ai compris du coup comme sin(i)=tan(i) on a :
Sin(i)= AB/BH=AB/AH et sin(i')= (n1sin(i))/n2=A'B'/A'H=AB/A'H
<=> (n1*AB)/(n2*AH)=AB/A'H
<=> A'H= n2*AH/n1 et donc A'A= AH-HA'= AH - n2*AH/n1= AH(n1-n2)/n1
La question suivante me demande de déterminer la distance à laquelle le chat perçoit le poisson mais sans la distance du poisson à la vitre c'est impossible non ?
A moins de juste répondre qu'il le perçoit à une distance de la vitre qui est 1/1,33 de sa distance réel à la vitre
D'accord avec ton message de 13h27
Concernant ton message de 13h33 : tu as raison, il faut connaître la distance du chat au dioptre.
Je te laisse faire un schéma approprié. Tu constateras que, pour le poisson, le chat paraît plus éloigné qu'il n'est réellement ; s'il est à 15cm du dioptre, son image virtuelle est à 19,95cm du dioptre comme obtenu à 00h22.
PS : évidemment, modéliser un chat par une flèche verticale est très simplificateur. L'essentiel à retenir : le poisson voit le chat plus éloigné qu'il n'est réellement ; le chat voit le poisson plus près qu'il n'est réellement.


