Niveau licence

Optique géométrique2

Posté par
toureissa 21-03-18 à 18:22

Bonsoir ,

C'est moi encore j'ai eu une difficulté avec la deuxième question de cet exo.

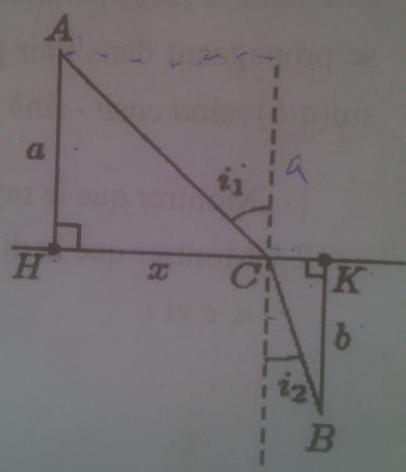
Un rayon lumineux se propage du milieu d'indice n₁ vers le milieu d'indice n₂.

1- Montrer que le chemin optique L_AB peut s'exprimer en fonction de n₁, n₂, a, b, x et h=HK.

2-On pose L_AB=f(x) , retrouver la loi de Snell-Descartes en appliquant le principe de Fermat qui prévoit que le chemin optique doit être minimal.

1- $L_{AB}=n_1×AC+n_2×CB$

$AC=\sqrt{a^2+x^2}$

$CB=\sqrt{b^2+(h-x)^2}$

$L_{AB}=n_1\sqrt{a^2+x^2}+n_2\sqrt{b^2+(h-x)^2}$

2-

$L_{AB}=f(x)=n_1\sqrt{a^2+x^2}+n_2\sqrt{b^2+(h-x)^2}$

Je doit chercher le minimum de cette fonction avec ses variations ?

Optique géométrique2

Posté par re : Optique géométrique2 21-03-18 à 19:13

J'ai eu : $f'(x)=\frac{n_1x}{AC}+\frac{n_2(x-h)}{CB}$

$x=atani_1$

$h-x=atani_2$

$AB=\frac{a}{cosi_1}$

$CB=\frac{b}{cosi_2}$

$f'(x)=n_1tani_1cosi_1-btani_2cosi_2$

$f'(x)=n_1sini_1-n_2sini_2$

$f'(x)=0\Leftrightarrow n_1sini_1=n_2sini_2$

Posté par re : Optique géométrique2 21-03-18 à 19:15

Bonjour
Tu dois effectivement calculer la dérivée par rapport à x et construire un rapide tableau de variations. Le cas particulier où L_AB est minimum est une situation conforme la la loi de Descartes.

Posté par re : Optique géométrique2 21-03-18 à 20:50

Nos derniers messages se sont croisés. En fait : tu n'avais pas besoin d'aide !

Posté par re : Optique géométrique2 21-03-18 à 23:46

Au départ je n'ai pas eu cette idée.

Merci beaucoup !

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Optique géométrique2

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique