Inscription / Connexion Nouveau Sujet
Optique géométrique - Télescope de Newton
Bonjour,
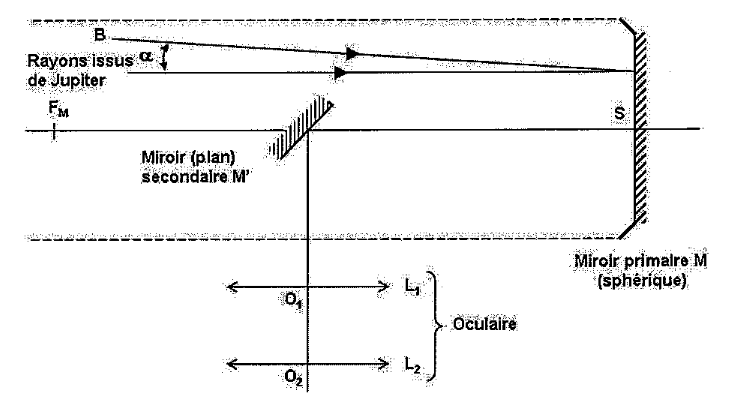
Je bloque sur un sujet d'optique géométrique portant sur le télescope de Newton (voir schéma).
Dans cette partie, on traite le télescope en entier (j'ai traité en amont une partie indépendante de celle-ci portant sur l'oculaire seul).
Énoncé :
Le rayon de courbure du miroir M est noté |R|.
L'axe principal du miroir M est dirigé vers le centre de Jupiter. Le point B correspond à un des bords de Jupiter, vu sous un diamètre apparent 2α (donc α de part et d'autre de l'axe).
Donner la taille de l'image A'B' donnée par le miroir M et de l'exprimer en fonction de |R| et α .
Là où j'en suis :
J'ai exprimé la formule de conjugaison pour un miroir sphérique, ainsi que le grandissement transversal. J'ai essayé des formules trigonométriques simples, mais j'ai l'impression qu'il me manque toujours une donnée... Je pense que je visualise mal la situation...
Je vous remercie par avance si vous avez quelques minutes pour m'aiguiller !
Voilà le schéma :
Bonjour
Tu peux, au moins "au brouillon", faire une figure représentant le miroir primaire seul et son foyer FM.
Puisque l'objet réel est à l'infini, dans quel plan se forme l'image ?Quelle est sa nature (réelle ou virtuelle) ?
Il suffit alors de tracer quelques rayons particuliers parallèles entre eux, émis par le bord supérieur de Jupiter pour avoir le rayon de l'image.
Merci pour votre réponse.
Comme l'objet réel est à l'infini , l'image se forme dans le plan focal image du miroir (et elle est réelle).
On a SFM = |R|/2 (car le miroir est sphérique)
Avec le schéma, je trouve :
tan(α)= α = A'B'/SFM
d'où A'B' = α |R| /2
Comme on a utilisé α (et non 2α), le A'B' que j'ai utilisé correspondrait à la taille du rayon de l'image (si j'ai bien compris). J'aurais donc tendance à la multiplier par 2 pour obtenir la taille demandée.
Le semblant de démarche vous semble-t-il cohérent ou suis-je complètement à côté ?
Le semblant de démarche vous semble-t-il cohérent ou suis-je complètement à côté ?
D'accord avec ton raisonnement ; tu as obtenu d'abord le rayon et ce qu'on appelle usuellement en optique la hauteur de l'image est en fait ici son diamètre.
Je vous remercie !
J'aurais une dernière question, si cela ne vous dérange pas... et si vous avez encore un peu de temps.
Énoncé :
Le miroir M' donne de A'B' l'image A''B'' que l'on observe grâce à l'oculaire.
M' est incliné à 45° sur l'axe principal du miroir M.
L'oculaire est placé de façon à ce que le centre de la lentille L1 soit à d = 5.5 cm du bord du tube du télescope, dont le diamètre est D = 20 cm.
On note O1Fo la distance entre le centre de la lentille L1 et le foyer principal objet Fo de l'oculaire complet.
A quelle distance du foyer principal FM du miroir M doit-on placer le centre du miroir M' pour que A''B'' soit dans le plan focal objet de l'oculaire ?
Là où j'en suis :
J'ai réalisé un schéma pour m'aider à y voir plus clair.
La distance entre le tube et le foyer objet de l'oculaire est :
d+O1Fo
Au vu des très nombreux angles dont on dispose, il y a très certainement des relations de trigonométrie à exploiter... mais je m'y perds rapidement et n'arrive pas à savoir dans quelle direction partir. Je vous remercie d'avance si vous pouvez m'aider !
Ne pas oublier les propriétés du miroir plan : celui-ci donne de A'B', image de Jupiter par la miroir concave et objet virtuel vis à vis du miroir plan, une image réelle A"B" symétrique de A'B' par rapport au plan du miroir plan. Il suffit donc que A"B" soit dans le plan focal de l'oculaire. Attention : la figure n'est pas à l'échelle : la distance de M' à FM est trop grande par rapport à la distance de M' à L1. Schémas ici :
![]()
Merci pour votre réponse et les schémas bien utiles que je découvre à l'instant !
J'avais bien compris les propriétés du miroir plan ainsi que le fait que A''B'' soit dans le plan focal de l'oculaire.
En revanche, je ne sais pas du tout comment répondre à la question, c'est-à-dire :
"A quelle distance du foyer principal FM du miroir M doit-on placer le centre du miroir M' pour que A''B'' soit dans le plan focal objet de l'oculaire ?"
Comment faire en sorte que la condition sur A''B'' soit respectée ?
J'ai utilisé les propriétés des miroirs sphérique et plan pour déduire la plupart des angles environnants, mais il est sans doute possible de procéder de manière plus simple et rigoureuse. Si vous avez d'autres pistes...
A" est le symétrique de A' par rapport au plan du miroir M'. Le symétrique de FM par rapport au plan du miroir M' doit être F1, le foyer objet de l'oculaire (ensemble {L1,L2}).



