Niveau licence

Optique géometrique : Stigmatisme d'une lentille plan convexe

Posté par
antonio30 02-05-17 à 22:47

Bonjour, je bloque sur un problème :

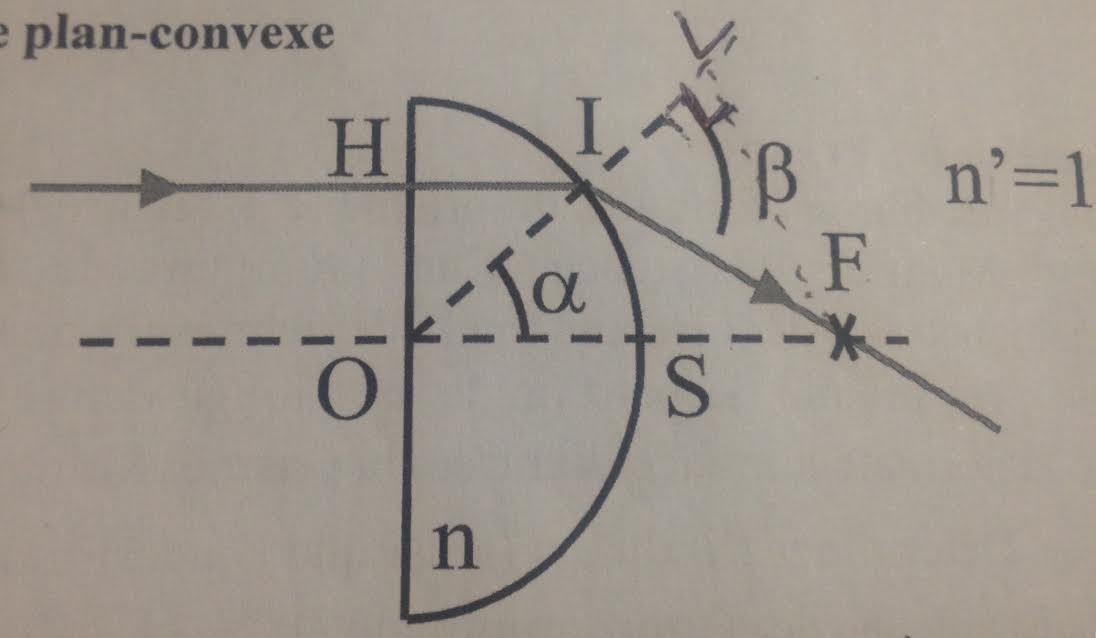
Une lentille est constituée par une une demi-sphère de rayon R et d'un verre d'indice n. Cette lentille reçoit perpendiculairement à sa face plane un faisceau de lumière parallèle couvrant complètement sa face.

1. On considère un rayon lumineux coupant en F l'axe du système après avoir traversé la lentille. Le rayon est défini par la valeur de l'angle correspondant. On pose OF=x. En utilisant les lois de Snell Descartes, calculer x en fonction de , ainsi que les valeurs minimale x_m et maximale x_M de x? En déduire que la lentille n'est pas rigoureusement stigmatique pour un point à l'inifni. Application numérique : n=1.52 et R=5 cm.

Un schéma du système optique est disponible en piece jointe.
On obtient donc OF=x et OI =R

1/ J'ai tout d'abord énoncé la loi de Snell Descartes dans ce cas là :
j'obtiens n*sin()=sin() ( car n'=1). Comme il faut calculer x en fonction de : j'ai dans un premier temps développé sin() en utilisant le point L que j'ai "inventé " dans le schéma de sorte que le triangle ILF est rectangle en L.
On a donc que sin()=LF/IF. Or on sait que OF=OI+IF donc IF =OF-OI=x-R donc sin()=LF/(x-R). Mais je ne sais pas comment me débarasser du LF.
Merci de votre aide .

$Optique géometrique : Stigmatisme d\'une lentille plan convexe$

Posté par re : Optique géometrique : Stigmatisme d'une lentille plan conve 02-05-17 à 23:47

Bonsoir
On peut s'intéresser au triangle (OIF) :
* l'angle aigu au sommet F vaut (-) ;
* le rapport sinus d'un angle sur longueur du côté opposé est constant dans un triangle quelconque (loi des sinus)...
Cela devrait t'aider. Je te laisse réfléchir...

Posté par re : Optique géometrique : Stigmatisme d'une lentille plan conve 03-05-17 à 12:26

Bonjour, excusez moi pour le retard de réponse j'ai suivi votre astuce, et je bloque quand même :
Dans un premier temps on a qu'au sommet F l'angle vaut (-) et au sommet I l'angle vaut (-). En utilisant, la loi des sinus je tombe sur : sin()/IF=sin(-)/x=sin(-)/d.
Comme sin(-)=sin().
Ma première méthode a été d'isoler sin() dans sin()/IF=sin(-)/x. Mais le problème est que sin() de la loi de Snell-Descartes s'annule. Je tombe sur n*sin()=sin()*x/(IF) et IF=x-R. Donc je rebloque à ce moment . Merci encore une fois de votre aide.

Posté par re : Optique géometrique : Stigmatisme d'une lentille plan conve 03-05-17 à 12:35

Je pense avoir trouvé un résultat. Je trouve cos()=1/2*(-x/(Rn²)+R/x+x/R). Je sais pas si je suis bon Merci

Posté par re : Optique géometrique : Stigmatisme d'une lentille plan conve 03-05-17 à 15:29

Ta méthode ne permet pas facilement d'isoler x. Comme tu l'as bien compris, le théorème des sinus permet d'écrire :

$\frac{x}{\sin\left(\beta\right)}=\frac{R}{\sin\left(\beta-\alpha\right)}=\frac{R}{\sin\left(\beta\right)\cos\alpha-\sin\left(\alpha\right)\cos\left(\beta\right)}$

En tenant compte de la loi de Descartes sur la réfraction :

$x=R\cdot\frac{n.\sin\left(\alpha\right)}{n.\sin\left(\alpha\right)\cos\left(\alpha\right)-\sin\left(\alpha\right)\cos\left(\beta\right)}$

En supposant $\alpha\neq0$ :

$x=R\cdot\frac{n}{n.\cos\left(\alpha\right)-\cos\left(\beta\right)}=R\cdot\frac{n}{n.\cos\left(\alpha\right)-\sqrt{1-n^{2}\cdot\sin^{2}\left(\alpha\right)}}=\frac{n\cdot R}{n.\sqrt{1-\sin^{2}\left(\alpha\right)}-\sqrt{1-n^{2}\cdot\sin^{2}\left(\alpha\right)}}$

Attention : pour les angles importants, le rayon ne ressort de la lentille que pour $n.\sin\left(\alpha\right)<1$ . Sinon, il y a réflexion totale.

Pour les angles très faibles (conditions de Gauss), on peut poser :

$\sin\left(\beta\right)=n.\sin\left(\alpha\right)\approx n.\alpha$

$\sin\left(\beta-\alpha\right)\approx\left(\beta-\alpha\right)\approx\left(n-1\right)\alpha$

Le théorème des sinus conduit ainsi à :

$x\approx\frac{n}{n-1}.R$

Remarque : on obtient le même résultat en considérant les deux cosinus comme très proches de 1 dans les conditions de Gauss.

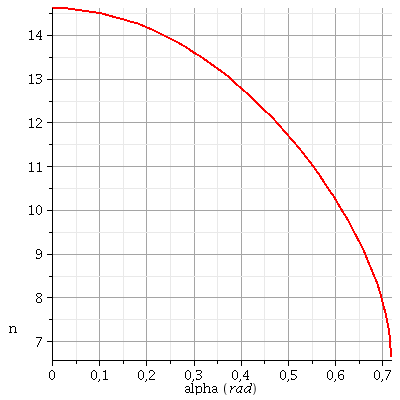
x est indépendant de l'angle alpha pourvu que celui-ci reste faible.

Pour les angles plus importants, il est facile de montrer que, lorsque $\sin^{2}\left(\alpha\right)$ augmente, la valeur de x diminue. La valeur de x dans les conditions de Gauss est donc en fait la valeur maximale possible de x. On obtient la valeur minimale en faisant tendre $n.\sin\left(\alpha\right)$ vers 1.

$x_{min}=\frac{n}{n.\sqrt{1-\frac{1}{n^{2}}}}.R=\frac{n}{\sqrt{n^{2}-1}}\cdot R$

Voici la courbe représentant les variations de x en fonction de alpha ci-dessous... x varie de 14,6cm à 6,64cm . On remarque aussi que la courbe est quasi horizontale pour alpha très faible : d'où les conditions de Gauss...

$Optique géometrique : Stigmatisme d\'une lentille plan conve$