Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths supForum Supérieur de maths sup PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths sup
Partager :

Optique géométrique - plaques d'immatriculation

Posté par
Honolulu17 25-10-18 à 16:28

Bonjour !

Je poste ce message car, après 3 heures de galère, je n'aboutis à rien !

Je bloque à une question de mon DM qui est utile pour toute la suite donc j'ai besoin de votre aide

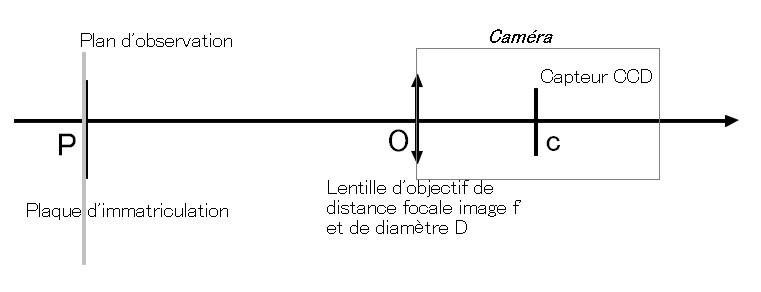
Le sujet parle d'une caméra qui contrôle les plaques d'immatriculation.

A.1 Donner la condition que doivent vérifier f' (distance focale image de la lentille) et PC (distance entre l'objet réel et son image réelle) pour que l'image se forme sur le capteur.

A.2 Exprimer la distance OC en fonction de L = PO et f' = OF'

Pour la question A1, je ne comprends pas s'il faut donner une condition réelle, en terme de longueur. Pour moi, il faut que PC soit supérieure à f'.

Pour la question A.2, je tourne en rond depuis 2 heures ...

Pour le moment, j'ai seulement les relations suivantes :

OC = PC - PO
\frac{1}{OC}=\frac{1}{OP}+\frac{1}{OF'}

J'ai essayer de remplacer PC par d'autres distances mais je retombe toujours sur OC = OC ...

Auriez - vous des pistes pour me débloquer ?

Merci beaucoup !

Bonne vacances

Optique géométrique - plaques d\'immatriculation

Posté par
vanoisere : Optique géométrique - plaques d'immatriculation 25-10-18 à 18:01

Bonjour
Considère la distance x = OC comme une inconnue puis écris la relation de conjugaison de Descartes en faisant intervenir uniquement x, PC et f'. tu vas tomber sur une équation du second degré en x. Pour qu'une solution réelle existe, le discriminant doit être positif : cela va te permettre de répondre à la première question.
Pour A2 : la relation de conjugaison de Descartes donne directement le résultat.

Posté par
Honolulu17re : Optique géométrique - plaques d'immatriculation 26-10-18 à 08:56

Bonjour,

Merci pour votre réponse !

Pour la relation de Descartes, celle de base est\frac{1}{OA'}-\frac{1}{OA}=\frac{1}{OF'}

Donc si je change avec les données de l'énoncé, j'obtiens \frac{1}{x}-\frac{1}{PO}=\frac{1}{f'} Puisque OA = OP mais du coup, je n'ai pas PC comme tu me dis de le faire apparaître ...
Faudrait que je mette ça ?  \frac{1}{x}-\frac{1}{PC-x}=\frac{1}{f'}
Mais je pense que je fais fausse route car je n'ai pas du tout une équation du seconde degré ...

Merci encore

Posté par
vanoisere : Optique géométrique - plaques d'immatriculation 26-10-18 à 10:45

Citation :
car je n'ai pas du tout une équation du seconde degré

Mais si , une fois mis au même dénominateur...
Attention aux signes : la loi de Descartes est valide en mesures algébriques : La mesure algébrique de OA est l'opposé de la distance (PC-x)

Posté par
Honolulu17re : Optique géométrique - plaques d'immatriculation 26-10-18 à 14:52

D'accord merci, donc j'ai mis (x - PC) à la place de (PC - x) mais je suis pas sûre, je n'arrive pas à bien visualiser le "sens" de la figure

Du coup j'arrive à la fin à [tex]\frac{-PC}{x^2-PCx}=\frac{1}{f'}

Ce qui donne :
- x^{2}+PCx - PC.f'=0[/tex]

et donc après je résous comme une équation normale et je trouve Delta = PC^2-4x(-1)x(-PC.f') Or il sera positif uniquement si f' est négatif mais du coup c'est logique puisque la lentille et convergente

Et pour la question 2, je réutilise cette équation ? Parce qu'il faut que je fasse "disparaitre" le PC et je n'y arrive pas

Merci

Posté par
vanoisere : Optique géométrique - plaques d'immatriculation 26-10-18 à 18:18

Citation :
- x^{2}+PC.x - PC.f'=0

OK mais il te faut revoir la notion de discriminant ! Ici :

\triangle=\left(PC\right)^{2}-4.PC.f'=PC.\left(PC-4f'\right)

L'équation admet une ou deux racine(s) réelle(s) pour :

\triangle\geq0\quad soit\quad PC\geq4f'

Posté par
Honolulu17re : Optique géométrique - plaques d'immatriculation 26-10-18 à 22:27

C'est avec le traitement, il a mis des x alors que je voulais mettre des x pour le produit !

Mais je vois pas du tout où ça mène ... c'est censé montrer que la lentille est convergente ?

Merci encore

Posté par
vanoisere : Optique géométrique - plaques d'immatriculation 26-10-18 à 22:46

La question A1 demande une  condition sur PC et f' pour qu'il soit possible d'obtenir une image... la voilà  !

Posté par
Honolulu17re : Optique géométrique - plaques d'immatriculation 29-10-18 à 09:24

Ok d'accord ! Merci beaucoup

Et donc pour la A2 je réutilise cette relation de conjugaison ... Je vais essayer tout ça, merci encore !

Posté par
Honolulu17re : Optique géométrique - plaques d'immatriculation 30-10-18 à 09:49

Pardon de encore vous déranger ... Pour la question A2, j'ai réutilisé la relation de conjugaison mais j'obtiens x en fonction x ...

\frac{1}{x}-\frac{1}{OP}=\frac{1}{f'} \Rightarrow \frac{OP-x}{OP.x}=\frac{1}{f'} \Rightarrow \frac{(OP-x)f'}{OP.x} = 1 \Rightarrow OP-x=\frac{OP-x}{f'} \Rightarrow x= -\frac{OP.x}{f'}+OP

J'ai voulu garder OP et f' puisqu'il faut que j'écrive x en fonction de ces 2 valeurs et mettre au même dénominateur mais je pense que je me suis plantée quelque part ...

Merci !

Posté par
Honolulu17re : Optique géométrique - plaques d'immatriculation 30-10-18 à 10:17

Je crois avoir compris mon erreur !!

\frac{1}{x}=\frac{1}{OP}+\frac{1}{f'} \Rightarrow \frac{1}{x}=\frac{OP+f'}{OP.f'} \Rightarrow x= \frac{OP.f'}{OP+f'}

Posté par
vanoisere : Optique géométrique - plaques d'immatriculation 30-10-18 à 10:56

Tu commets la même erreur de signe qu'au début : la formule de conjugaison est algébrique :

\dfrac{1}{\overline{OC}}-\dfrac{1}{\overline{OP}}=\dfrac{1}{f'}

avec :

\overline{OC}=OC=y (la lettre « x » a déjà été utilisée dans le problème)

\overline{OP}=-OP=-L

donc :

\dfrac{1}{y}+\dfrac{1}{L}=\dfrac{1}{f'}

Posté par
Honolulu17re : Optique géométrique - plaques d'immatriculation 31-10-18 à 18:19

Arf j'ai pas fait attention ... Si je garde le symbole "algébrique" tout au long de l'exercice ça convient ?
J'ai fait l'exercice avec l'équation

Honolulu17 @ 30-10-2018 à 10:17



\frac{1}{x}=\frac{1}{OP}+\frac{1}{f'} \Rightarrow \frac{1}{x}=\frac{OP+f'}{OP.f'} \Rightarrow x= \frac{OP.f'}{OP+f'}

en notant la "barre" au-dessus des lettres.

Mais si j'applique ta formule, j'arrive à y=\frac{f'.L}{L-f'} et j'obtiens sensiblement les mêmes résultats dans la suite de l'exercice ...  je vais modifier ce qu'il faut !

Merci beaucoup

Posté par
vanoisere : Optique géométrique - plaques d'immatriculation 31-10-18 à 20:23

Dans la mesure où f' est nettement inférieur à L, les deux applications numériques conduisent à des résultats analogues mais : autant faire un raisonnement correct !

Posté par
Honolulu17re : Optique géométrique - plaques d'immatriculation 01-11-18 à 10:47

Bien sûr ! Merci beaucoup de ton aide


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !