Inscription / Connexion Nouveau Sujet
optique géométrique
bonjour, dans un dm voila la question que j'ai :
1) Une ampoule (supposée ponctuelle) est accrochée à 0,5 m du plafond d'une salle haute de 3m. Elle est située juste au dessus d'un miroir plan posé au sol. Ce miroir plan est circulaire et son diamètre est de 25 cm. En justifiant votre réponse décrivez la zone du plafond (forme et dimensions) qui va être éclairée par la réflexion dans le miroir.
2. On souhaite que la zone éclairée au plafond ne contienne pas l'ombre de l'ampoule et on place pour ce faire une cale à la périphérie du miroir sans le déplacer. Le miroir devient donc penché par rapport à l'horizontale. Quelle est l'épaisseur minimale de la cale pour satisfaire le souhait exprimé? Justifier.
et j'ai du mal pour la première question : voila ce que j'ai trouver sur internet :" (25 cm / 0,5 m) * 3 m = 150 cm
Donc, la zone du plafond éclairée par la réflexion dans le miroir sera une ellipse d'environ 25 cm de large et 150 cm de haut."
mais je n'ai pas du tout compris son raisonnement (je peux vous copié collé toute son explication si vous voulez mais je n'ai pas compris)
après personnellement voila mon raisonnement :
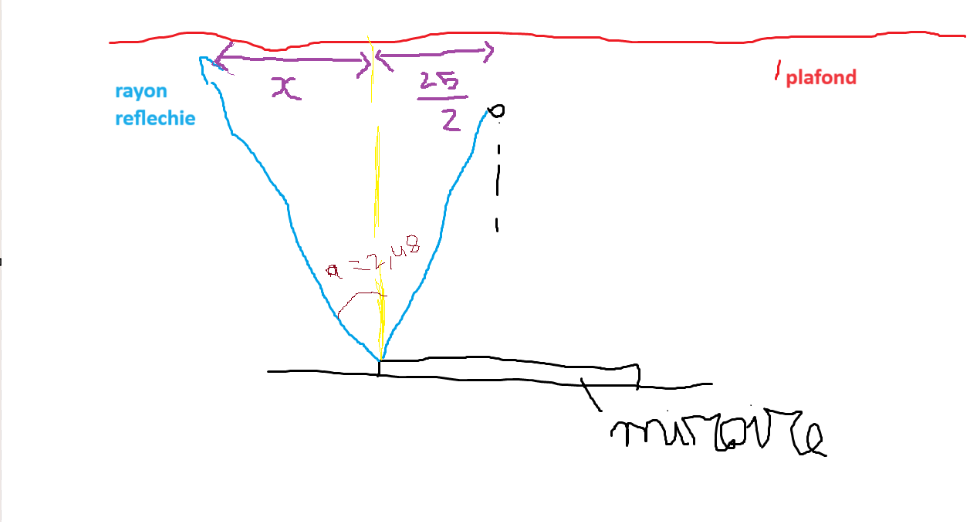
soit a l'angle entre le rayon incident a l'extrémité du miroir et la normal du miroir donc tan(a) = (25/2)/( 3-0.5)=0.05
donc a = arctan(0.05) = 2.86
donc l'angle du rayon réfléchi avec la normal sera aussi 2.86
et posons x le coté opposée donc tan(2.86) = x/3
donc x = 3 * tan(2.86) = 0.14m et x + 25/2 = 26.5 cm
donc la zone éclairée et un cercle de rayon de 26.5m
(j'ai essayé comme j'ai pu de schématisé ca avec paint^^')
Bonjour
Pas facile de faire un schéma soigné avec un logiciel que l'on ne connait pas bien ! Tu peux parfaitement faire un schéma propre sur une feuille de papier. Ensuite, tu le scannes et le postes ici. (Cliquer sur l'icône "Img")
Tu peux parfaitement faire un schéma propre sur une feuille de papier. Ensuite, tu le scannes et le postes ici. (Cliquer sur l'icône "Img")
Sinon, pour t'aider dans tes calculs : n'oublie pas qu'un miroir plan donne d'un objet réel (ici l'ampoule) une image virtuelle, symétrique de l'objet par rapport au plan du miroir. Les rayons réfléchis peuvent être tracés comme s'ils provenaient de cette image virtuelle. Cela facilite l'application du théorème de Thalès...
a ok, je pense avoir compris, voila selon Thalès Ducoup j'ai ceci :
(0.25/2)/x = 0.5/3 donc
x = ((0.25/2)*3) = 0.75 m
x est le rayon donc il y a une tache lumineuse de 150 cm de diamètre sur le plafond (et le reste du plafond est éclairée)
merci 
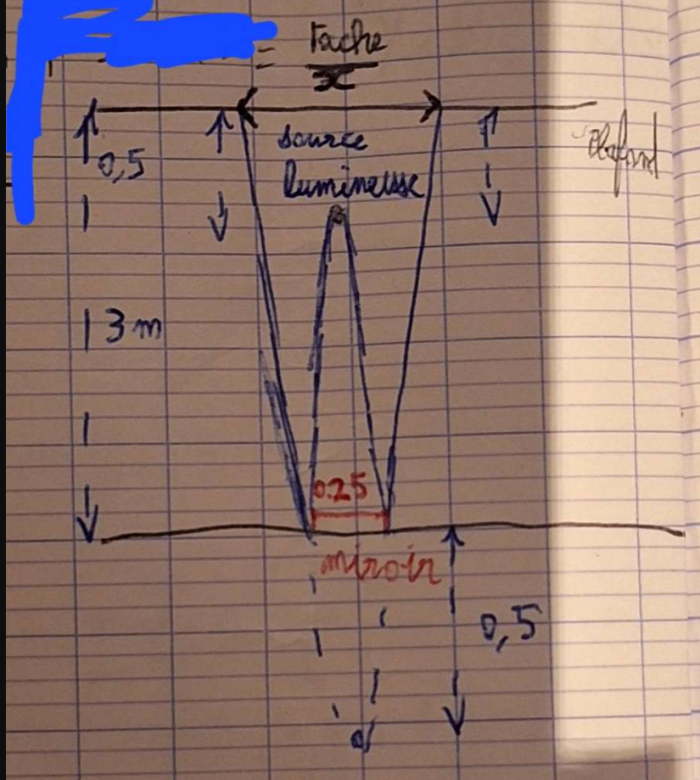
L'idée générale est bonne mais la source virtuelle A' est le symétrique de la source réelle A (l'ampoule) par rapport au plan du miroir. Si on pose h=3m la hauteur de la pièce et d=0,5m la distance du plafond à l'ampoule A, A' est ainsi à la distance h-d= 2,5m sous le plan du miroir.
Autre chose : peux-tu fournir la référence du site où se trouve le corrigé de la question deux ? Il y a peut-être un schémas clair sur lequel s'appuyer...
a oui ok ducoup x = (((0.25/2)*3)/2.5) = 0.15 donc l'ombre est de 30cm de diamètre
par contre pour le 2 je n'ai vraiment aucune idée 
donc l'ombre est de 30cm de diamètre
Ce n'est pas ce que j'obtiens. Impossible de vraiment t'aider car tu ne justifies pas ton raisonnement. Comme déjà écrit, il faut faire un schéma soigné, le publier ici, puis justifier ton raisonnement en t'aidant de mes précédents messages. Sans justification, un résultat n'a pas de valeur !
voila le schéma en claire juste je réécris mon raisonnement ici parce que c'est vrai mon écriture est pas très belle  :
:
Posons B le centre du miroir et C le centre de la "tache lumineuse" le théorème Thalès nous dit : taille du miroir / taille de l'ombre = A'B / A'C <=> 0.25/x = 2.5/5.5 <=> x = (0.25*5.5)/2.5 = 0.55 m donc le diamètre de la tache lumineuse est 55cm
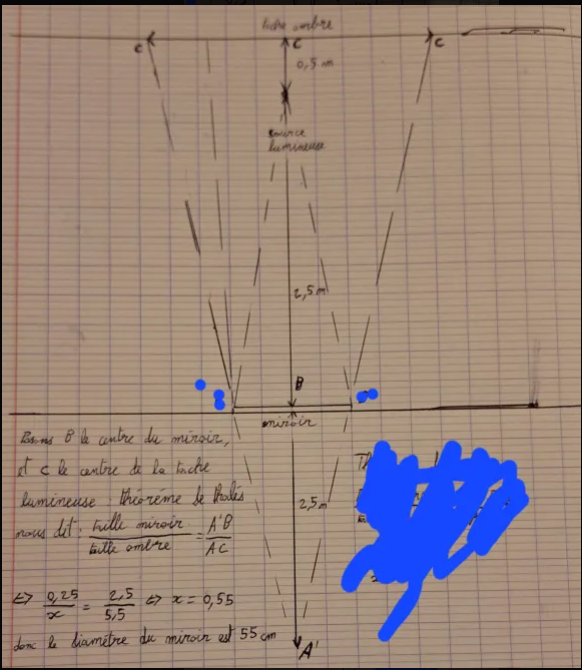
D'accord avec toi maintenant ! 
Je te joins mon schéma : pratiquement le même que le tien ; il contient juste quelques lettres supplémentaire pour faciliter les explications.
Pour être bien clair et préparer la réflexion sur la question 2 : que voit-on précisément au plafond ?
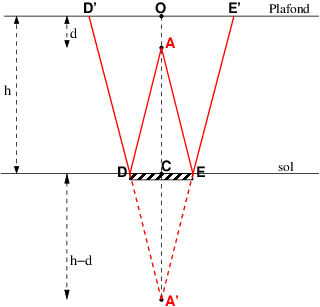
Pour être bien clair et préparer la réflexion sur la question 2 : que voit-on précisément au plafond ?
au plafond on voit une partie éclairée grâce au miroir et une partie sombre qui est l'ombre de la lampe
je pense qu'il faudrait que le rayon arrive au plafond sans "être interrompu" par la lampe comme dans l'image
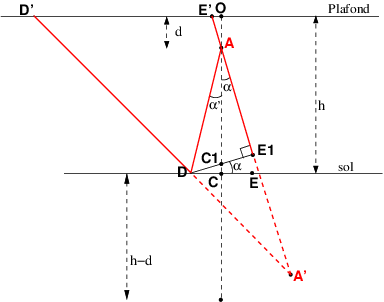
Je pense qu'il faut bien comprendre la situation 1 avant d'étudier la situation 2. Ton schéma ou le mien trace les rayons extrêmes passant par les bords D et E du miroir mais les autres rayons émis par A, réfléchis en des points compris entre D et E, arrivent au plafond en des points compris entre D' et E'. De plus, la figure est invariante par rotation autour de l'axe vertical passant par les points A et C : conséquence : on voit au plafond un disque lumineux de centre O et de diamètre D'E'=55cm.
Il y a tout de même une exception concernant le rayon AC perpendiculaire au miroir. Ce rayon se réfléchit sur lui-même de sorte que ce rayon lumineux réfléchi est arrêté par l'ampoule. Il n'y a pas de lumière en O . O constitue l'ombre de A au plafond. L'ampoule n'étant en réalité pas rigoureusement ponctuelle, on voit au plafond le disque lumineux de centre O et de diamètre D'E' avec une très petite tache sombre en O : l'ombre de l'ampoule.
Ce qu'il faut retenir pour la suite : l'ombre de l'ampoule au plafond est sur la perpendiculaire au miroir passant par A.
Question 2 : supposons que l'on fasse tourner dans le sens trigonométrique le miroir autour d'un axe perpendiculaire au plan de figure passant par D. Faire tourner le miroir d'un angle  pour un rayon incident AD fixe fait tourner le rayon réfléchi DD' d'un angle 2
pour un rayon incident AD fixe fait tourner le rayon réfléchi DD' d'un angle 2 alors que la normale au miroir passant par A et servant à repérer la position de l'ombre tourne seulement de l'angle
alors que la normale au miroir passant par A et servant à repérer la position de l'ombre tourne seulement de l'angle  . Puisque A' se déplace aussi vers la doite du schéma, E' va se déplacer vers la gauche. Bref : quand on augmente progressivement
. Puisque A' se déplace aussi vers la doite du schéma, E' va se déplacer vers la gauche. Bref : quand on augmente progressivement  ,la tache lumineuse se déplace vers la gauche plus vite que l'ombre de l'ampoule. Le cas limite à étudier est donc le cas où l'ombre, situé sur la normale au miroir passant par A se confond avec le point E'. La figure ci-dessous correspond à ce cas limite.
,la tache lumineuse se déplace vers la gauche plus vite que l'ombre de l'ampoule. Le cas limite à étudier est donc le cas où l'ombre, situé sur la normale au miroir passant par A se confond avec le point E'. La figure ci-dessous correspond à ce cas limite.
A noter que l'inclinaison décrite ici augmente la distance D'E' sans augmenter la largeur de la tache lumineuse mesurée suivant une perpendiculaire au plan de figure. La tache lumineuse est maintenant elliptique.
Je te laisse réfléchir à tout cela... Ce n'est pas très simple... Essaie de bien comprendre la figure et de calculer la valeur de  . Tu auras facilement alors la hauteur EE1 de la cale.
. Tu auras facilement alors la hauteur EE1 de la cale.
il y a des petits morceaux que j'avoue ne pas avoir bien compris 
on voit au plafond un disque lumineux de centre O et de diamètre D'E'=55cm.
ce disque il est sombre non ?
la tache lumineuse se déplace vers la gauche plus vite que l'ombre de l'ampoule.
c'est a dire qu'on arrive plus facilement a "illuminé" le plafond (en mettant une cale) ?
alors pour ce qui de alpha je n'ai pas eu trop de difficulté : j'ai utilisé CV (comme dans mon dessin que j'ai repris de ton plan) qui est la moitié du miroir qui est le coté opposé de alpha et CV qui est le coté adjacent de alpha :
donc
mais par contre pour ce qui est de [EE1] j'avoue que j'ai beau retourné le problème je ne trouve vraiment pas

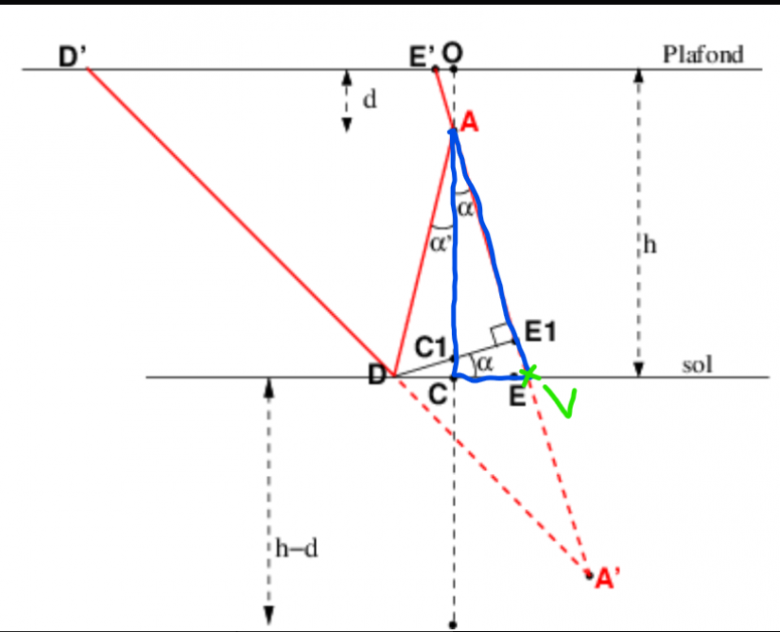
on voit au plafond un disque lumineux de centre O et de diamètre D'E'=55cm.
Je n'ai sans doute pas été assez précis à ce sujet. Imagine pour commencer l'ampoule allumée sans miroir au sol. L'ampoule envoie de la lumière dans toutes les directions y compris au plafond qui n'apparaît donc pas noir. Plaçons maintenant le miroir sans cale (question 1). Celui-ci réfléchit la lumière qu'il reçoit vers le plafond de sorte que la surface du plafond recevant cette lumière réfléchis reçoit deux fois plus de puissance lumineuse par unité de surface que le reste du plafond. Cette zone apparaît donc très lumineuse et le reste du plafond, par contraste, apparaît plus sombre. En absence de cale, cette zone très lumineuse est un disque de diamètre D'E'=55cm. Au centre O de ce disque, il n'y a pas de lumière réfléchie car celle-ci est arrêtée par l'ampoule . C'est l'ombre de l'ampoule.
Question 2 :
la tache lumineuse se déplace vers la gauche plus vite que l'ombre de l'ampoule.
Mettre une cale sous le bord droit du miroir incline celui-ci d'un angle
 , ce qui déplace la tache lumineuse au plafond vers la gauche. Puisque cette tache lumineuse se déplace plus vite vers la gauche, on va obtenir un cas limite où l'ombre sera sur le bord gauche E' de la tache lumineuse. C'est la situation que j'ai schématisée.
, ce qui déplace la tache lumineuse au plafond vers la gauche. Puisque cette tache lumineuse se déplace plus vite vers la gauche, on va obtenir un cas limite où l'ombre sera sur le bord gauche E' de la tache lumineuse. C'est la situation que j'ai schématisée.
Puisque le diamètre du miroir est très petit devant la hauteur de l'ampoule (h-d), on peut prévoir
 petit (moins de 10°) et utiliser ainsi les approximations usuelles :
petit (moins de 10°) et utiliser ainsi les approximations usuelles :
sin(
 )
) tan(
tan( ) et cos(
) et cos( )
) 1
1
Soit sur ta figure le triangle (DVE1) rectangle en E1 :
DV=DE1/cos(
 )
) DE1 : diamètre du miroir = DE.
DE1 : diamètre du miroir = DE.
Les points E et V sont donc pratiquement confondu en réalité. Attention, pour obtenir un minimum de clarté au niveau du schéma, j'ai fortement exagéré la valeur de
 .
.
Tu devrais être capable de terminer maintenant.
Cela n'est pas demandé par l'énoncé mais, pour mieux comprendre pourquoi l'ombre de l'ampoule disparaît au plafond si l'angle d'inclinaison du miroir dépasse la valeur  de la question 2, je te refais un schéma en choisissant un angle d'inclinaison
de la question 2, je te refais un schéma en choisissant un angle d'inclinaison  >
> . On remarque que la perpendiculaire AH au plan du miroir ne rencontre plus le miroir. La lumière émise par l'ampoule suivant la direction AH n'est donc pas réfléchie vers le plafond : donc pas d'ombre de l'ampoule au plafond !
. On remarque que la perpendiculaire AH au plan du miroir ne rencontre plus le miroir. La lumière émise par l'ampoule suivant la direction AH n'est donc pas réfléchie vers le plafond : donc pas d'ombre de l'ampoule au plafond !
On remarque aussi que la tache lumineuse due à la lumière réfléchie s'est encore davantage décalée vers la gauche. Sa largeur D'E' mesurée dans le plan de figure a aussi augmenté. Cela accentue le caractère elliptique de la tache lumineuse car la largeur de la tache, mesurée suivant la perpendiculaire au plan de figure, est la même qu'à la question 1 : 55cm.
Si tu disposes chez toi d'un miroir plan équivalent à un disque, tu peux facilement reproduire ces expériences.
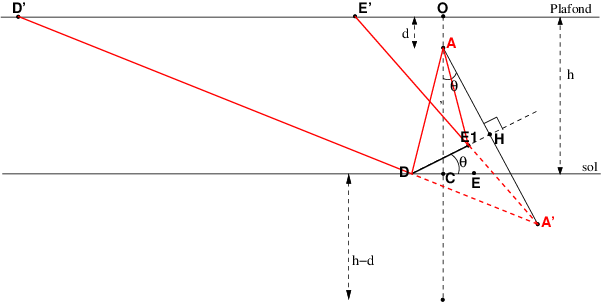
a ok alors si j'ai bien compris
en tout cas merci beaucoup c'est ultra claire  !!! je pense j'y serais jamais arrivais seul XD
!!! je pense j'y serais jamais arrivais seul XD
Attention à ne pas oublier l'unité. Cela donne bien une hauteur de cale de 1,25cm.
C'est vrai que cet exercice n'est pas facile, d'où l'intérêt d'un bon schéma !
Reprend le schéma et le contenu du message du 18-01-24 à 22:07.
L'approximation a été justifiée par le fait que l'angle est suffisamment petit pour considérer cos(
)=1. En revanche, illel a commis un oubli que je n'avais pas relevé : les deux distances doivent avoir la même unité : le centimètre par exemple. Cela conduit à
 =2,86°.
=2,86°.
Les angles étant petits : donc :
Dans le message de hillel, il s'agit de tan(2,86) et non tan(0,48), les angles étant mesurés en degrés mais il s'agit sûrement d'une étourderie de copie puisque le reste est correct.


