Inscription / Connexion Nouveau Sujet
Optique géométrique
Bonjour à tous et merci de me lire
J'ai un soucis en optique s'il vous plaît
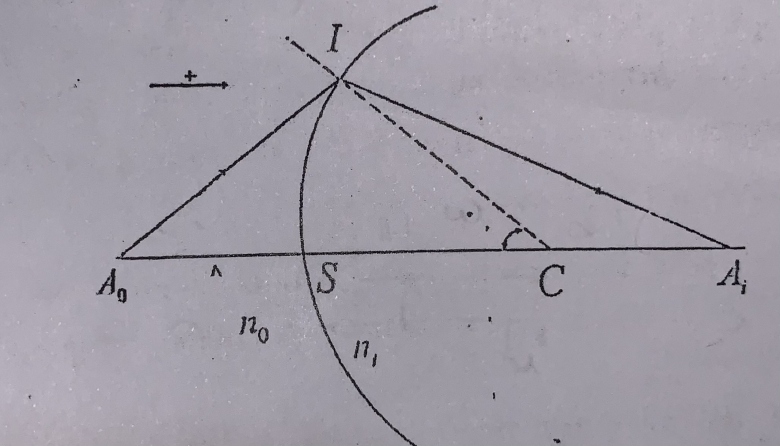
On considère le dioptre sphérique d'indice no et ni et le couple de point Ao et Ai sur l'axe Sz. Montrer que le chemin optique L entre Ao et Ai s'écrit: L=
Où do=|SAo| di=|SAi| p=|SC| (Je n'arrive pas à mettre le symbole de mesure algébrique.Mais toutes ces valeurs absolues sont valeurs absolues des mesures algébriques) et w=ICS(l'angle ICS)
J'ai pu démontrer cela
En introduisant, dans l'expression précédente, les quantités algébriques p0=SAo pi=SAi et R=SC(toutes ces quantités sont des mesures algébriques ie mesure algébrique de SAo égale à p0),établir:
a)Que le sommet S est sa propre image
J'ai un soucis à ce niveau j'ai posé d0=0 et di=0 afin de calculer le chemin optique de S à S mais je ne trouve pas un résultat nul afin de conclure. Je ne pense pas également avoir la bonne méthode
b)Que le centre C est sa propre image
Ici également j'ai ce soucis. En fait pour ces deux questions je me demande si on doit réellement déduire des précédentes
Merci beaucoup
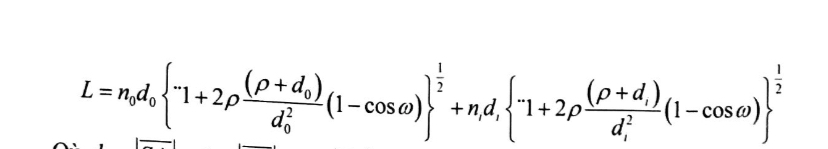
Bonjour
mais je ne trouve pas un résultat nul afin de conclure
La condition de stigmatisme est-elle L=0 ? Revois si nécessaire ton cours sur le sujet.
La condition de stigmatisme est L=cte
Je me disais que dans ce cas ça devrait donner 0 car le point est le même
Raison pour laquelle je voulais avoir 0 mais en remplaçant d0 et si pr 0, j'obtiens un chemin qui dépend de w encore
Ah D'accord w=0 et le 1-cosw devient nul
Et concernant le centre s'il vous plaît c'est le cas qui m'a plus dérangée
Le résultat est immédiat physiquement : tout rayon passant par C traverse le dioptre sans déviation.
Sinon, ton expression de L n'est pas assez générale, elle ne prend pas en compte le fait que les trajets virtuels correspondent à des longueurs de chemin optique négatives.
Ici :
L=n1. -no.
-no. indépendant de
indépendant de  .
.
D'accord merci beaucoup c'est compris
Une dernière question svp
Tout cela signifie que pour tous points P et Q si L(PQ)=cste alors P et Q sont conjugués il y'a stigmatisme rigoureux ?
Je pensais que la propriété était si P et Q sont conjugués alors L(PQ)=cste
C'est plus une question de logique mathématique à ce niveau. J'aimerais en fait savoir s'il y'a suffisance ou nécessité ou alors équivalence svp
Il y a équivalence...
Attention : en physique, le stigmatisme n'est souvent qu'approché (voir conditions de Gauss).