Inscription / Connexion Nouveau Sujet
optique geometrique
bonjour,
un exercice fait en TD mais a cause d'une panne de trin J'ai seulement la correction et aucune explication.
une ige de profondeur h est fichée sous le flotteur que l'on modelisera comme un disque mince de rayon R. A quelle condition cette tige est elle invisible de la surface ? on prendra n=1,33 pour l'indice de l'eau.
R
<----->
__________----------------__________
|
| la tige de hauteur h
|
j'ai dis qu'une partie des rayons etait bloque par le flotteur. on se retrouve avec un triangle contenat tout les rayons bloqué par le flotteur mais je n'arrive pas trop a voir comment determiner l'angle. ( dans la correction on note que sin=R/racine(R^2+h^2) , je vois comment on l'obtient mais je ne vois pas trop par ou commencer .)
ensuite une partie des rayons passe mais sa ne nous interrese pas.
je dis que tout les rayon avec un angle d'incidence superrieur a teta crit ne seront pas percu a cause de la reflexion totale mais pour sa il nous faut un angle d'incidence egale a pi/2.
on applique la formule n1sinO1=n2sinO2 or sinO1=1 puisque O1=pi/2
n1=n2sinO2 implique que n1/n2=sinO2 donc que arc sin (n1/n2)=O2
j'obtient O2=48,75 degrée.
pouvez vous m'expliquez pour l'angle sous le flotteur?
merci d'avance.
n1.sin(i1) = n2.sin(i2)
1 * sin(i1) = 1,33.sin(i2)
sin(i2) = 1/1,33 * sin(i1)
sin(i2) <= 1/1,33
i2 <= 48,75°
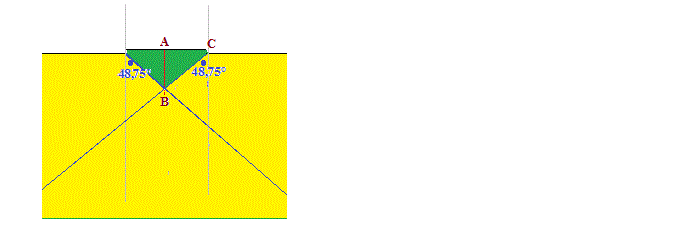
Il est possible de la surface de voir la zone en jaune.
Il est impossible de la surface de voir la zone en vert.
Donc la tige sera invisible de la surface si sa longueur est inférieure à la hauteur du triangle vert dessinée en rouge sur mon dessin.
Dans le triangle vert : angle ABC = 48,75° (alterne interne avec ...)
AC = BC.sin(ABC)
et BC² = AB² + AC² = h² + R²
R = RCarrée(h²+R²) * sin(ABC)
sin(ABC) = R / RCarrée(h²+R²)
R / RCarrée(h²+R²) = sin(48,75°) = 1/1,33
Cette relation permet de calculer h , longueur de la tige sous laquelle elle sera invisible de la surface.
Sauf distraction. 
merci, mais est-ce que tu pourrais me réexpliquer ce que tu a fais au debut pour trouver sin(i2 )?
la condition pour laquelle la tige est invisible est qu' h doit etre inferieur a la hauteur qu'on a calculé ?
n1.sin(i1) = n2.sin(i2)
Avec :
n1 = 1, l'indice de réfraction de l'air.
i1 l'angle d'incidence du rayon mumineux (forcément compris entre 0 et 90°)
n2 = 1,33, l'indice de réfraction de l'eau
i2 l'angle de réfraction du rayon dans l'eau
1 * sin(i1) = 1,33 * sin(i2)
sin(i2) = (1/1,33) * sin(i1)
comme 0 <= sin(i1) <= 1 -->
sin(i2) <= 1/1,33
---------
"la condition pour laquelle la tige est invisible est que h doit être inférieur à la hauteur qu'on a calculé ?"
Yes.

bonjour, maintenant je bloque sur la ddeuxieme partie :/ (j'ecrit que sin(abc)=sin Ocrit)
sin Oc=1/1,33=R/Rcarrée(R^2+h^2)
je développe et j'obtient h=Rcarrée((n2^2-n1^2 )R^2/n1^2) est ce le bon resultat ?
on m'a explique une méthode par la tangente en projettant le triangle dans un cercle orthonormée, on dis que tan Oc =sin Oc/cos Oc et que sinOc=R=1/1,33 et cos Oc=h
on obtient R/h = sin Oc/cos Oc =1/1,33 //Rcarrée(1-sinOc) mais j'ai le probleme je n'arrive pas a développer
merci d'avance


