Inscription / Connexion Nouveau Sujet
optique géometrique
bonjour,
Je bloque sur l'exercice suivant,
On considere un dioptre plan séparant l'air d'indice n.a d'un milieu d'indice n .
donner la formule littérale de i1, angle d'incidence tel que le rayon réfracté soit perpendiculaire au rayon réflechi.
Montrer que i1 > 45°. Calculer i1 avec n.a= 1.00 et n = 1.33 (eau).
Je sais qu'il faut utiliser la formule de Descartes mais je ne vois absolument pas comment determiner que i1 soit > 45° .....
Je ne demande pas la réponse juste un coup de pouce.
merci d'avance
Bonjour
Ce qui se conçoit bien se dessine bien 
Donc un petit crobard est souvent utile.
Sur le fond, ce n'est la LA formule mais LES formules que tu dois utiliser, celle pour la réfraction et celle pour la réflexion, tu vas ainsi relier les 3 angles du problème dans 2 équations ... Puis tu pose la condition de perpendicularité.
Est ce plus clair?
ah ...
Appelons donc i1 l'angle du rayon incident, i2 celui du rayon réfracté dans le milieu d'indice n, et r celui du rayon réfléchi
Attention: en optique il faut prendre bien soin d'orienter les angles
La loi de la réflexion te dit donc que i1 = -i2
La loi de la réfraction te dit que sin(i1) = n.sin(r)
Tu as donc 2 équations pour 3 angles
Ensuite l'énoncé t'impose une relation entre i2 et r: les rayons réfléchis et réfractés doivent être orthogonaux ...
C'est plus clair? Je fais tout pour ne pas te donner la réponse
et je ne veux pas la reponse, je n'en vois pas l'utilité, par contre la loi de refraction ce n'est pas plutot:
sin i1 = n.sin i2 ?
Autant pour moi, j'ai interverti les angles ... je suis de nature étourdie ... je réécris ... en faisant attention
La loi de la réflexion te dit donc que i1 = -r
La loi de la réfraction te dit que sin(i1) = n.sin(i2)
Ouf!
- i2 ? Comment arrives tu à cette conclusion? J'en arrive à une différente ... Un petit schéma comme suggéré initialement ...
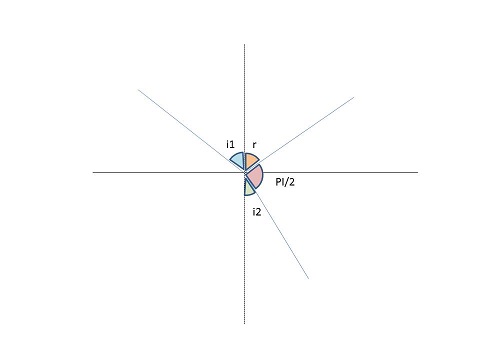
c'est à mon tour d'avoir été tete en l'air ... je voulais metre (pi)/2 à la place (pi).. si c'est cela ?..
néanmoins, quand je remplace
-r = (pi)/2 - i2 dans la deuxieme equation j'arrive grace aux formules d'additions de trigo à
n= cos i2 ce qui n'est logique
Euh ... je ne vois pas trop comment arrives à cela:
tu as
En combinant (2) et (3) tu exprimes en fonction de
et tu remplaces dans (1) tu arrives à un équation qui imposes bien
Donc en exprimant i2 en fonction de i1 :
-r+ i2 = (pi)/2
dc i2 = (pi)/2 + r or r = -i1 donc i2 = (pi)/2 - i1
en remplacant dans sin (i1) = n. sin(i2)
sin (i1) = n. sin ( pi/2 - i1 ) ?
moi j'avais utilisé la formule sin ( a-b) ce qui me donnait quelque chose de incoherent, d'ailleurs quand utiliser sin ( a -b ) ou sin (pi/2 - x )?
j'ai trouver 53.06 pour i1
ça doit être la même chose ou presque ...
Annuler
connectez vous