Inscription / Connexion Nouveau Sujet
Optique Formules de conjugaison - Descartes et Newton
Bonjour!
J'ai besoin de votre aide pour une petite démonstration que je ne parviens pas à faire:
Démontrez que les formules de conjugaison de Newton se déduisent algébriquement des formules de Descartes en utilisant la relation de Chasles: Pour des points A, O et F d'une droite orientée d: AO= AF + FO.
J'ai essayé en appliquant la relation de Chasles à la formule de Descartes mais je ne parviens pas à retomber sur la formule de Newton!
Merci de votre aide!
Bonjour Liloulilice,
il me semble qu'on a deja fait des affaires ensemble, a propos d'un exercice sur le champ d'un miroir plan... en octobre dernier...
Pour gagner du temps, je vais poser OA = p, OA' = p', OF' = f' OF = - f', FA = x, F'A' = x'. Toutes ces grandeurs sont bien entendu algebriques.
Prenons par exemple le cas d'une lentille mince (mais la demo ci-dessous peut etre reproduite pour n'importe quel systeme centre) :
Relation de Descartes : -1/p + 1/p' = 1/f'.
Relation de Chasles : p' = OA' = OF' + F'A' = f' + x' ; de meme, p = OA = x - f'.
Donc -1/(x - f') + 1/(x' + f') = 1/f' = (x - x' - 2f')/[(x - f').(x' + f')]. Ou encore f'(x - x' - 2f') = (x - f').(x' + f').
Je te laisse developper ca toi-meme, et tu trouveras x.x' = -f'2, relation de Newton.
NB : la demonstration en utilisant les triangles semblables est encore plus rapide.
Si tu as des questions, n'hesite pas.
Prbebo.
Merci beaucoup! Est-ce que vous pourriez me parler plus en détails de cette démo avec les triangles semblables?
PS: en effet, je crois que vous m'aviez déjà aidé pour l'optique! Là, je suis en train de réviser car j'ai l'examen d'optique bientôt!
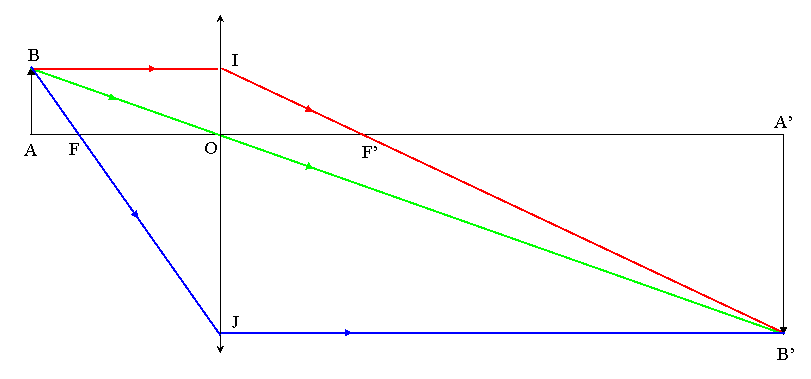
pas de probleme. Suis avec la figure ci-dessous, toujours en prenant le cas d'une lentille mince :
1) Les triangles FOJ et FAB sont semblables (ce sont deux triangles rectangles avec les angles AFB et OFJ egaux, donc leurs trois angles sont egaux). Thales donne OJ/AB = FO/FA. J'ai ecrit ca en gras car si on projette FO et FA sur l'axe optique on a FO > 0 et FA < 0 ; de meme si on projette AB et OJ sur un axe vertical oriente par exemple vers le haut, alors AB > 0 et OJ < 0. Les deux raports ci-dessus sont donc algebriques et, ici, negatifs.
Avec les notations deja vues dans le post precedent, FO = + f' et FA = x ; d'autre part, OJ = A'B' : donc A'B'/AB = f'/x.
2) Les triangles F'OI et F'A'B' sont eux aussi semblables, donc A'B'/OI = F'A'/F'O = x'/(-f'). Et de meme, OI = AB, donc A'B'/AB = -x'/f'.
L'egalite des deux resultats donne bien f'/x = -x'/f', soit x.x' = -f'2. De plus cette methode fournit aussi le grandissement transversal : A'B'/AB = f'/x = -x'/f'.
On peut facilement verifier que ce resultat, obtenu sur un cas de figure particulier (objet et image reels) peut etre retrouve sur n'importe quel autre cas de figure.
Si tu as d'autres problemes en optique, n'hesite pas.
Prbebo.