Bonjour à tous.
Il s'agit d'étudier un réfractomètre. Je n'ai pas trop de mal à répondre dans l'absolu aux questions, mais le problème se trouve dans les angles orientés...Je ne sais pas trop comment m'y prendre il semblerait...
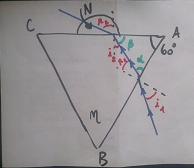
Il s'agit tout d'abord d'exprimer l'angle d'incidence i₂ sur la face AC en fonction de l'angle réfractée de la face AB r₁. On introduit pour plus de facilité les angles et , et on sait (alors la je parle en angles non orientés, sinon je me trompe...) = 90 - r₁ et = 90 - i₂ et on sait que l'angle en A est égale à 60°. Par conséquent, + + 60 = 180 -i₂ - r₁ + 60 = 0 i₂ = 60 - r₁. OR d'après la correction, i₂ = 60 + r₁. C'est là que je soupçonne les angles orientés d'entrer en jeu...

On veut déterminer l'indice N de la goutte d'eau sur la face AC, sachant que l'angle réfracté r₂ sur la face AC est égale à 90° lorsque i₁ = -8°. (On connait n = 1.6).
D'après Snell-Descartes, on a r₁ = arcsin(sin(-8)/n) -5°. Donc i₂ = 60 - 5 = 55 (en angles non-orientés) soit 55°. Et Nsin(r₂) = nsin(i₂) . Et sin(r₂) = 1, donc N = 1.6sin(55) 1.31.

Donc ma question serait de savoir pourquoi  i₂ = 60 + r₁ et de par la même occasion, vérifier si N est correct...
Voilà, je vous souhaite une bonne journée et merci d'avance