Bonjour chloe1210,

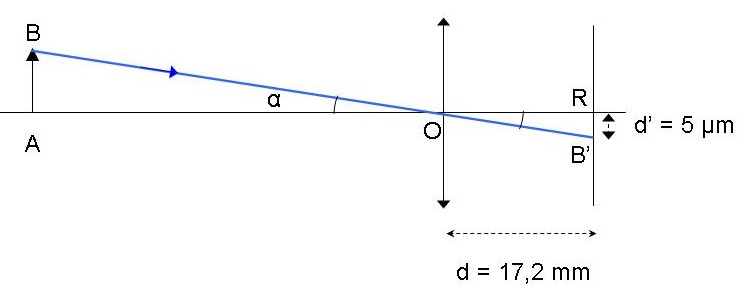
aucune difficulté. Regarde le schéma ci-dessous :

L'oeil est ramené à la lentille équivalente de centre optique O, et au plan de la rétine situé à la distance OR = d. Cet oeil regarde un objet AB dont le pied A est sur l'axe optique. Quelle que soit la distance à laquelle se situe cet objet, l'image de A se trouve en R (à la fois dans le plan de la rétine et sur l'axe optique). L'image B' de B, elle, se trouve sur le trajet du rayon lumineux qui est arrivé sur la rétine en passant par O (donc sans être dévié). OK ?

Pour que l'oeil puisse distinguer les extrémités de l'objet AB il faut que leurs images, R et B', tombent sur deux cellules rétiniennes différentes, donc que RB' soit à d'.
L'angle sous lequel on voit AB est donc tel que tan = d'/d = radians. On obtient 2,91.10^-4 radians, ce qui correspond à peu près à une minute d'angle (1/60^ième de degré).

L'angle AOB s'appelle "diamètre angulaire de l'objet" ; sa valeur minimale s'appelle "pouvoir de résolution angulaire".

Pour avoir une idée de ce que représente , imagine un livre placé à la distance de l'oeil OA = 25 cm (quasiment au punctum proximum) : la taille de cet objet est alors AB = OA.tan = 72 micromètres (pas loin de 1/10^ième de mm).

Si tu as des questions n'hésite pas.

Bonjour chloe210,

est-ce que ma réponse a répondu à ta question, ou faut-il revenir sur cet exercice ?