Inscription / Connexion Nouveau Sujet
(Optique) Descartes
Bonjour, je rencontre des problèmes dans un exercice qui requiert les lois de Descartes:
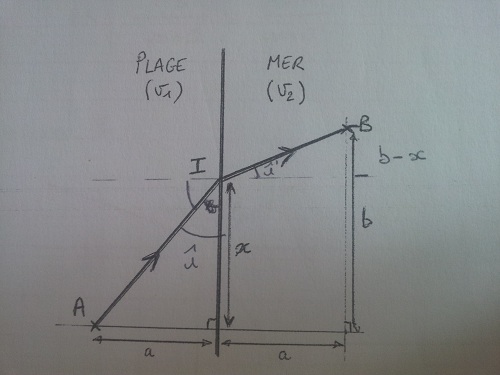
Un sauveteur situé en A doit secourir un nageur situé en B. Sur la plage, il court à vitesse constante v1, dans l'eau il nage à la vitesse constante v2<v1.
Son temps de trajet dépend de l'endroit I où il se jette à l'eau (repéré par la variable x)
Montrer que ce temps de trajet est minimal pour une certaine valeur x=x0 avec:
x0/(v1
(x0²+a²) = (b-x0)/v2[(b-x0)²+a²]
c'et pas très dur.
Le trajet est minimal si i et i' vérifie la loi de Descartes : n1.sin(i) = n2.sin(i')
Alors c'est quoi n1 et n2 ici ? Si on prend une vitesse arbitraire c (équivalent de la vitesse de la lumière dans le vide en optique), alors tu sais que n1 = c/v1, idem pour n2. Du coup tu appliques la formule de Descartes. Tu fais un peu de géométrie pour trouver les expressions des sinus, et tu simplifies par c de chaque côté.
Annuler
connectez vous