Inscription / Connexion Nouveau Sujet
Optique cristalline,surface d'indice
Bonsoir,je post ce message car je n'ai pas compris le corrigé de cet exo d'optique cristalline certain point ne sont pas clairs,le voici:
Deux prismes et un cube sont taillé dans un cristal positif dont les indices sont (1.4;1.6)avec une surface d'indice dont la projection de l'ellipsoïde sur le plan
contenant l'axe optique donne l'ellipse jointe au verso(il n'y a rien au verso,je sais pas pourquoi).
1)Faire une représentation des surface d'indice pour l'axe optique dans le plan et pour l'axe optique perpendiculaire au plan.
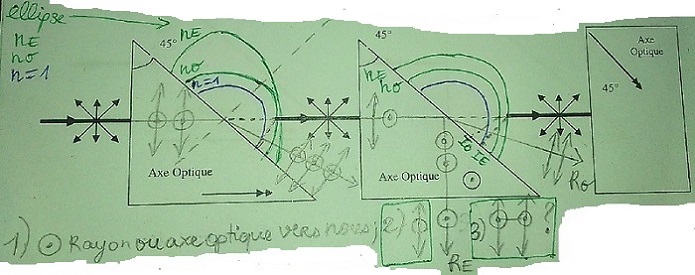
2)Compléter le parcours des rayons suivant avec les directions de polarisation.
Et voici(en bas) le corrigé de mon profs:
Cependant je me demandais,cette ellipsoïde qui devient une ellipse(en vert) en projetant,c'est la surface d'indice de quoi?
Même question pour les cercle vert et bleu des prismes 1 et 2.
Ensuite j'aurai voulu savoir comment on sait que les rayons "sorte" ainsi du prisme,et comprendre la signification des "rond avec les flèches (voir 1);2);3) sur photo1)", de "" et "
" sur la photo.
Enfin à quoi servent les indications "cristal positif" et les indice 1.4,1.6?
Je vous remercie d'avance pour vos réponses à toutes ces questions.
PS:deux des photos sont quasiment identique,j'ai mis les deux au cas ou vous ne comprenez pas l'écriture de la dernière photo.
Bonjour,
Pas question de faire un cours sur la biréfringence ici. Tu trouveras quelques renseignements sur ce site : ![]() ; les schémas, page 4 en particulier, sont clairs. Je trouve juste dommage qu'il note
; les schémas, page 4 en particulier, sont clairs. Je trouve juste dommage qu'il note  l'indice ordinaire classiquement noté no et
l'indice ordinaire classiquement noté no et  l'indice extraordinaire classiquement noté ne. La biréfringence du cristal est la différence :
l'indice extraordinaire classiquement noté ne. La biréfringence du cristal est la différence :  n=ne-no. Ton énoncé précise que le cristal est positif : ne>no ; donc : ne=1,6 ; no=1,4. Si on calcule les angles de réfraction limite pour ces deux indices, on obtient respectivement :
n=ne-no. Ton énoncé précise que le cristal est positif : ne>no ; donc : ne=1,6 ; no=1,4. Si on calcule les angles de réfraction limite pour ces deux indices, on obtient respectivement :  e=arcsin(1/1,6)
e=arcsin(1/1,6) 38,7° ;
38,7° ;  o=arcsin(1/1,4)
o=arcsin(1/1,4) 45,6°. Il faut évidemment remarquer qu'une valeur est inférieure à 45°, l'autre supérieure... Revois ton cours d'optique géométrique sur la réflexion et la réfraction...
45,6°. Il faut évidemment remarquer qu'une valeur est inférieure à 45°, l'autre supérieure... Revois ton cours d'optique géométrique sur la réflexion et la réfraction...
Ellipsoïde des indices. Tu trouveras dans ton cours la définition mathématique. Pratiquement à quoi çà sert ? Soit une direction de propagation d'une lumière polarisée rectilignement dans le cristal, caractérisée par un vecteur  . Imagine l'intersection de l'ellipsoïde avec le plan perpendiculaire à la direction (O,
. Imagine l'intersection de l'ellipsoïde avec le plan perpendiculaire à la direction (O, ) La distance du point O à l'ellipsoïde dans une direction donnée représente la valeur de l'indice dans cette direction de polarisation de la lumière. (attention : ne confond pas direction de propagation et direction de polarisation de la lumière...)
) La distance du point O à l'ellipsoïde dans une direction donnée représente la valeur de l'indice dans cette direction de polarisation de la lumière. (attention : ne confond pas direction de propagation et direction de polarisation de la lumière...)
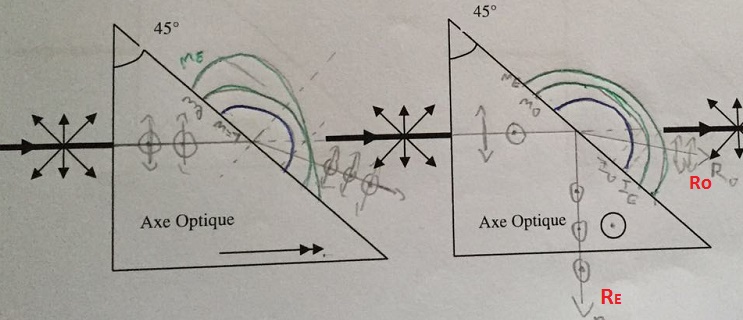
Application à ton exemple n° 1 : La direction de propagation de la lumière est celle de l'axe optique du cristal, c'est à dire celle de l'axe de symétrie de ton ellipsoïde. L'intersection de cette ellipsoïde avec un plan perpendiculaire à la direction de propagation est un cercle de rayon no ( sur la figure 2 du document page 3). Conséquence : l'indice ne varie pas en fonction de la direction de polarisation : le prisme se comporte comme s'il n'était pas biréfringent : si on essaie d'appliquer la seconde loi de Descartes sur la réfraction au second dioptre, le fait que l'angle d'incidence vaut 45° conduit à : no .sin(45°)=sin(r) avec r angle de réfraction. Le calcul conduit à r
sur la figure 2 du document page 3). Conséquence : l'indice ne varie pas en fonction de la direction de polarisation : le prisme se comporte comme s'il n'était pas biréfringent : si on essaie d'appliquer la seconde loi de Descartes sur la réfraction au second dioptre, le fait que l'angle d'incidence vaut 45° conduit à : no .sin(45°)=sin(r) avec r angle de réfraction. Le calcul conduit à r 81,9° : la lumière émergeante n'est pas polarisée et est déviée vers la base du prisme. Logique : l'angle d'incidence de 45° est inférieur à l'angle de réfraction limite
81,9° : la lumière émergeante n'est pas polarisée et est déviée vers la base du prisme. Logique : l'angle d'incidence de 45° est inférieur à l'angle de réfraction limite  o déjà calculé.
o déjà calculé.
Application à ton exemple n° 2 : la direction de propagation est perpendiculaire à l'axe optique ; par rapport au cas précédent, le cercle est remplacé par une ellipse de demi grand axe ne et de demi petit axe no. La lumière polarisée parallèlement à l'axe optique se comporte comme si le prisme était d'indice o : l'angle de réfraction sur le second dioptre vaut 45° ; elle émerge du prisme en étant déviée vers la base comme dans le premier cas. La lumière polarisée perpendiculairement à l'axe optique se comporte comme si le prisme est d'indice ne. Pour cette lumière, l'angle d'incidence (45°) est supérieur à l'angle de réfraction limite  e. Cette lumière polarisée subit donc une réflexion totale à 90° suivant les lois de Descartes sur la réflexion...
e. Cette lumière polarisée subit donc une réflexion totale à 90° suivant les lois de Descartes sur la réflexion...


