Inscription / Connexion Nouveau Sujet
Optique - Concours
Bonjour, j'aurai besoin d'aide, j'ai fais un exercice, pouvez-vous corriger mes réponses s'il vous plait :
Partie A
Utilisation d'un viseur :
Les lentilles sphériques minces, considérées dans cette partie et notées (Li), sont utilisées dans le
cadre de l'approximation de Gauss. Chaque lentille (Li) est caractérisée par son centre optique Oi et
par sa distance focale image i'. Les foyers objet et image sont notés respectivement Fi et Fi'.
La formule de conjugaison de Descartes (1) précise la position, sur l'axe optique, des points
conjugués A et A' :
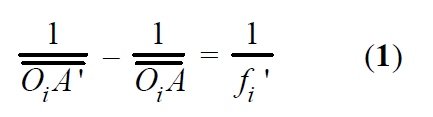
La formule de conjugaison de Newton (2) précise la position des points A et A' par rapport aux
foyers :
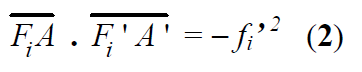
Un viseur « à frontale fixe », noté (V ), est un système centré comprenant trois éléments de même
axe optique :
- un objectif constitué d'une lentille mince (L1) convergente ;
- un réticule de centre R (lame à faces parallèles d'épaisseur négligeable sur laquelle sont
gravés deux traits orthogonaux formant une croix) ;
- un oculaire constitué d'une lentille mince (L2) convergente.
Le réticule est situé entre ces deux lentilles, à la distance d1 de (L1) et à la distance d2 de (L2)
(figure A.1).
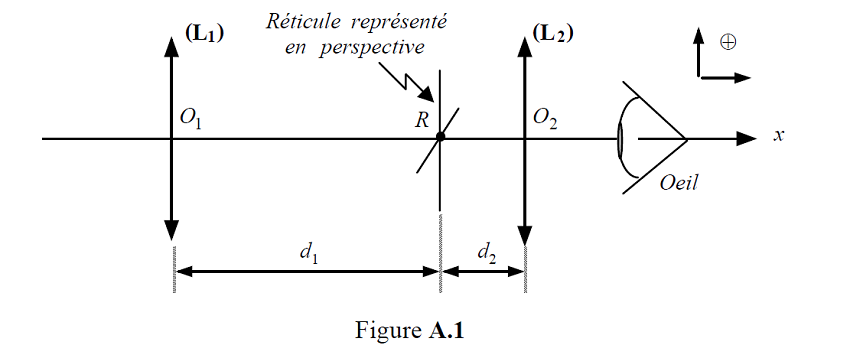
Données : 1' = + 8,0 × 10-2 m ; 2' = + 3,0 × 10-2 m ; d1 = + 15 × 10-2 m.
I. Caractéristiques du viseur
1. Déterminer la distance d2 = RO2 pour qu'un oeil emmétrope, c'est-à-dire « normal », puisse
observer l'image du réticule, à travers (L2), sans accommoder (dans ce cas l'image, renvoyée à
l'infini, peut être observée avec netteté et sans fatigue oculaire).
2. Soit un ensemble de rayons lumineux incidents passant tous par le point F, foyer principal objet
du viseur (V ) . Donner la principale caractéristique géométrique du trajet de ces rayons
lorsqu'ils émergent de (V ) .
3. Proposer le tracé d'un pinceau lumineux issu de F et qui émerge du viseur (V ) .
4. Déterminer la position du foyer principal objet F de (V ) , en calculant la grandeur algébrique F1F .
Réponses :
1) En utilisant La formule de conjugaison de Descartes, on a :
d2 = (f'1 - d1) / (d2 * f'1)
2) Ils émergents parallèlement à l'axe optique.
Je répondrais aux autres questions pour plus de lisibilité.
Merci !
Bonjour Damien130008,
je ne vois pas comment tu as pu trouver cette reponse a la premiere question : pour que l'oeil normal puisse voir le reticule sans accommoder, il suffit que l'image du reticule donnee par (L2) soit a l'infini, donc que le reticule soit dans le plan focal objet de (L2). On trouve donc, arithmetiquement, d2 = f'2.
Pour que le viseur fonctionne bien, il faut qu'on puisse voir simultanement l'image d'un objet et celle du reticule ; comme l'image du reticule est a l'infini, il faut que l'image finale de cet objet soit aussi a l'infini, d'ou sa place en F. Mais si l'image finale de l'objet est a l'infini, c'est que son image intermediaire (donnee par (L1)) se trouve dans le plan focal objet de (L2), cad superposee au reticule. On en conclut que le foyer objet F du viseur et l'objet dont l'image donnee par (L1) est en R.
En appelant x et d1 les distances arithmetiques respectivement entre F et O1 et entre O1 et R, la relation donnant x se tire de l'equation de conjugaison :
(-1)/(-x) + 1/d1 = 1/f'1, ce qui donne x = 17.14 cm.
Je suppose que la suite de l'exercice etait de calculer x : voila, c'est fait ! Ok pour ta reonse a la question 2.
Si tu as des questions n'hesite pas.
Prbebo.