Inscription / Connexion Nouveau Sujet
optique
Bonjour ,
Quelqu'un aurai t-il la gentillesse de m'aider sur mon exercice, je suis bloquer.
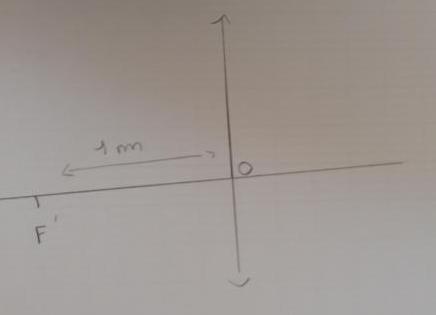
Une lentille convergente de 1m de distance focale est disposée de façon que son axe principal soit dirigé vers le centre du Soleil.
1. Déterminer la position de l'image du Soleil donnée par cette lentille, ainsi que la grandeur du diamètre α' de cette image A'B'. Diamètre apparent du Soleil: 32 minutes d'arc.
2. A 242 mm de cette image, on dispose un écran sur lequel on veut obtenir une image réelle et agrandie de la première image A'B' du Soleil. On utilise pour cela une lentille convergente de 2 cm de distance focale. Quelle doit être la position de cette lentille et quelle est la grandeur du diamètre de cette dernière image?
Bonjour
Tu pourrais commencer par faire un schéma clair de la situation que tu pourrais poster sur le forum. Explique ce que tu as fait et ce que tu ne comprends pas. Plus facile de t'aider ensuite.
Un peu sommaire non ? Sans indication du sens de propagation de la lumière, impossible de savoir si le foyer image F' est bien placé. Et le foyer objet F ?
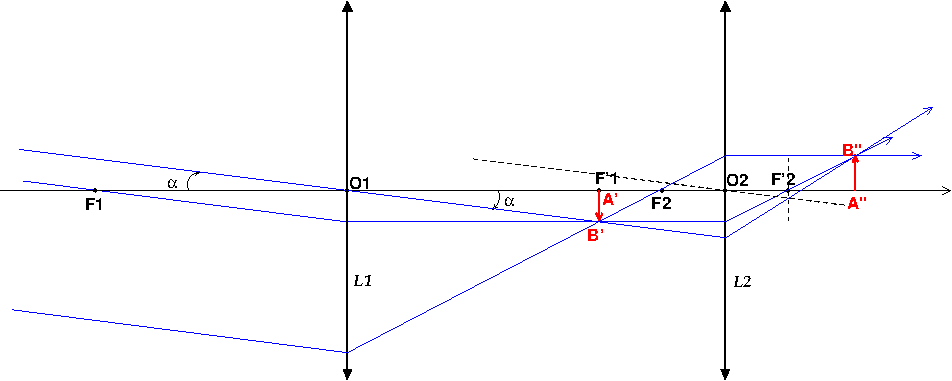
Le soleil est suffisamment éloigné pour être assimilable à un objet réel à l'infini : tous les rayons émis par un point du soleil et reçus par la lentilles sont parallèles entre eux. Pour obtenir un schéma simple, tu peux imaginer que le "point bas" du soleil est à l'infini et sur l'axe optique. Où convergeront ces rayons après traversée de la lentille ?
Les rayons émis par le point haut du soleil et reçus par la lentille forment un faisceau de rayons parallèles entre eux mais inclinés de l'angle  par rapport à l'axe optique,
par rapport à l'axe optique,  désignant le diamètre angulaire du soleil vu de la lentille. Où convergeront ces rayons ? ...
désignant le diamètre angulaire du soleil vu de la lentille. Où convergeront ces rayons ? ...
Je te laisse faire un schéma de tout cela et répondre aux questions (au moins à la première).
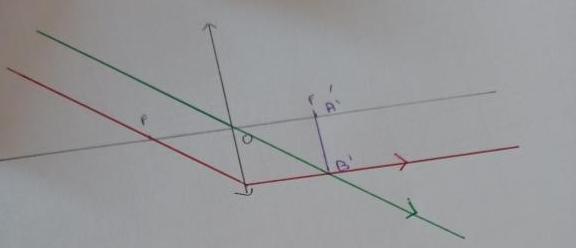
C'est ça le schéma ?
C'est une image réelle et inversés.
Cependant je ne vois pas comment on peut déterminer alpha'
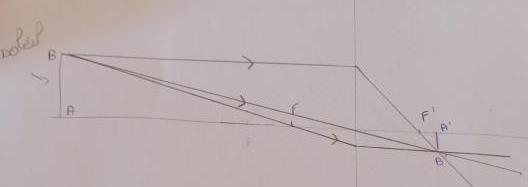
Ton schéma correspond à l'image réelle par une lentille convergente d'un objet réel situé à distance finie. Ce n'est pas du tout la situation ici !
Tout me semble expliqué en détail dans mon précédent message. Relis attentivement ce message et fais la figure en conséquence. La notion de diamètre angulaire du soleil (ou diamètre apparent  ) y est définie.
) y est définie.
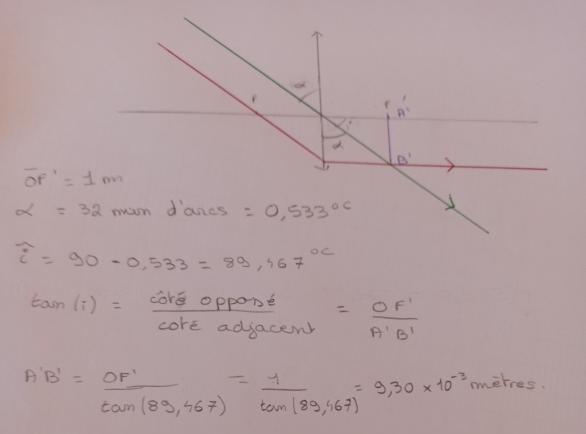
Oui ! Avec  : angle entre les rayons incidents que tu as tracés et l'axe optique. Il te reste à déterminer A'B' qui est le diamètre de l'image du soleil par la lentille.
: angle entre les rayons incidents que tu as tracés et l'axe optique. Il te reste à déterminer A'B' qui est le diamètre de l'image du soleil par la lentille.
Tu as commis deux erreurs consécutives dont les effets se compensent de sorte que tu obtiens le bon résultat.
Le diamètre angulaire (appelé aussi diamètre apparent  ) est l'angle entre les rayons incidents et l'axe optique. C'est l'angle que tu appelles "i" sur ta figure.
) est l'angle entre les rayons incidents et l'axe optique. C'est l'angle que tu appelles "i" sur ta figure.
Tu devrais savoir qu'une lentille ne donne une image d'une netteté correcte que dans les conditions de Gauss. Cela suppose des rayons incidents peu incliné par rapport à l'axe optique, pas incliné de presque 90° !
Puisque tu te trompes ensuite en exprimant la tangente en fonction de f' et A'B', tu obtiens au final le résultat correct.
Pour la deuxième question, on sait que OF'=2 cm et que A'A=242mm mais je ne sais pas comment savoir la position de la lentille ?
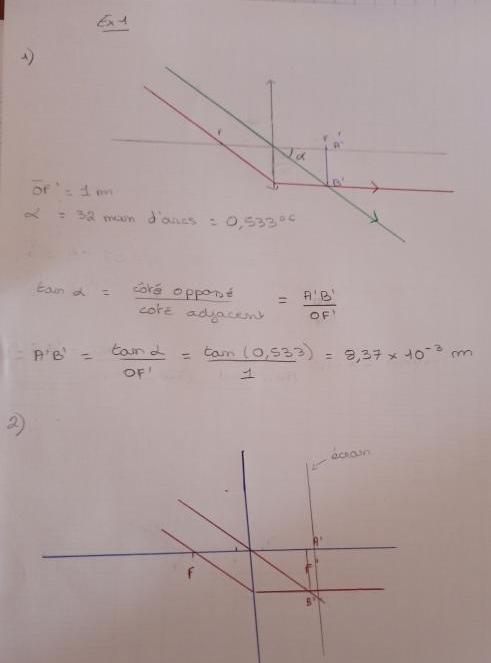
Pour la deuxième lentille de distance focale f'2=20mm, l'image A'B' du soleil par la première lentille se comporte comme un objet dont l'image par la deuxième lentille est A"B" avec A'A''=242mm.
Pour construire cette image, tu peux partir de ton dernier schéma en le complétant par la deuxième lentille, cela en t'inspirant de la figure faite dans ton message du 18-03-20 à 15:59 .
Ensuite, il faut utiliser la formule de conjugaison puis celle du grandissement.
Relation de conjugaison :
1/O'A'' = 1/OA' + 1/O'F''
O'A'' = (O'F'' * OA') / (O'F'' + OA')
Mais on ne connait pas OA' ? (OF''=20 mm)
Relation de grandissement
A''B''/A'B' = O'A''/OA'
A''B''=(O'A''/OA')/A'B'
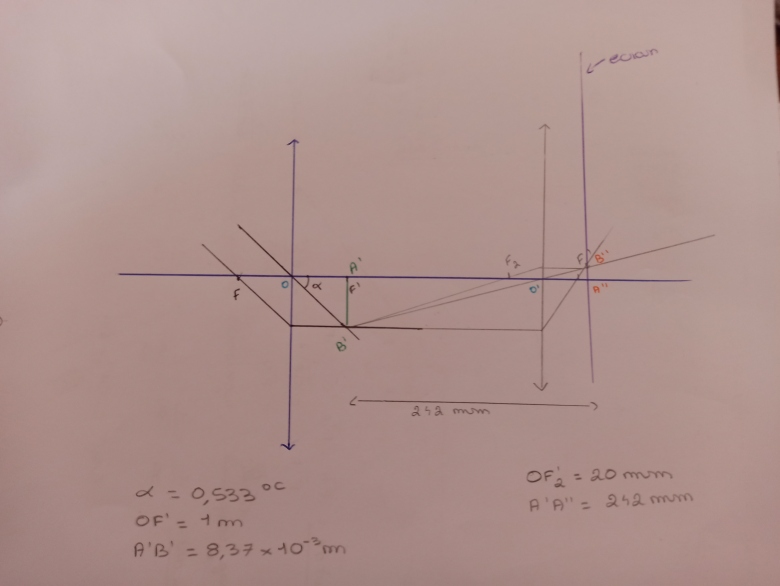
Ton schéma est correct. J'y ai rajouté le rayon passant par le centre de la première lentille.
La formule de conjugaison que tu as écrite fait intervenir deux inconnues : O2A' et O2A".
Tu peux aussi écrire :
Cela te fait un système de deux équations à deux inconnues. Facile ensuite d'obtenir le grandissement donc la distance A”B”.