Inscription / Connexion Nouveau Sujet
Optique
Bonjour !
Je sollicite votre aide pour une question que je ne comprends pas dans un exercice d'optique voilà l'énoncé :
On assimile l'objectif d'un appareil photo à une lentille mince convergente .
Lorsqu'un appareil photo est mis au point sur un objet A, l'image forme une tâche due à la taille g des pixels du capteur.
Établissez en s'appuyant sur une figure, l'expression de la distance hyperfocale H, c'est à dire la distance entre le point A et la lentille pour que, mettant au point à la distance H, la tâche image d'un point à l'infini reste incluse dans un pixel.
Exprimer H en fonction de g, f' et D le diamètre du diaphragme de l'objectif.
Selon moi la distance hyperfocale serait donc la distance la plus faible à laquelle je pourrais rapprocher le point A pour que le point A apparaisse net ET qu'un objet à l'infini apparaisse net aussi. Est-ce juste?
En fait je ne comprends pas ce que signifie "En mettant au point à la distance H".
Bonjour
Selon moi la distance hyperfocale serait donc la distance la plus faible à laquelle je pourrais rapprocher le point A pour que le point A apparaisse net ET qu'un objet à l'infini apparaisse net aussi. Est-ce juste?
Oui ! Tu supposes donc l'appareil photo réglé pour obtenir une image nette lorsque l'objet est à l'infini. La distance objectif - capteur est donc f'. Tu rapproches alors progressivement l'objet A, supposé sur l'axe optique, de l'objectif. L'image de A, noté A', se forme sur l'axe optique, un peu derrière le capteur. L'ensemble des rayons issus de A traversant la lentille rencontrent le capteur à l'intérieur d'un disque de centre F' donc il est facile de calculer le diamètre par application du théorème de Thalès. Il suffit d'écrire que ce diamètre vaut g dans le cas particulier où la distance AO vaut H. (O : centre de la lentille).
La relation de Thalès nécessite de déterminer au préalable la distance p'=OA' à partir de la relation de conjugaison.
Commence par faire une figure propre dans le cas limite H=AO.
Je te laisse réfléchir... N'hésite pas à poster à nouveau si tu ne t'en sors pas !
Ok merci beaucoup pour ces précisions !
J'ai fais plusieurs figures et je comprends presque tout mis à part que je n'arrive pas à visualiser sur ma figure le diamètre du disque de convergence de tous les rayons en A'.
J'ai bien le point A' qui se forme un peu derrière le capteur mais sur ma figure ci dessous ou se trouve ce disque ? (J'ai bien conscience qu'il n'apparait pas car mon dessin est "à plat" mais alors comment faire ?
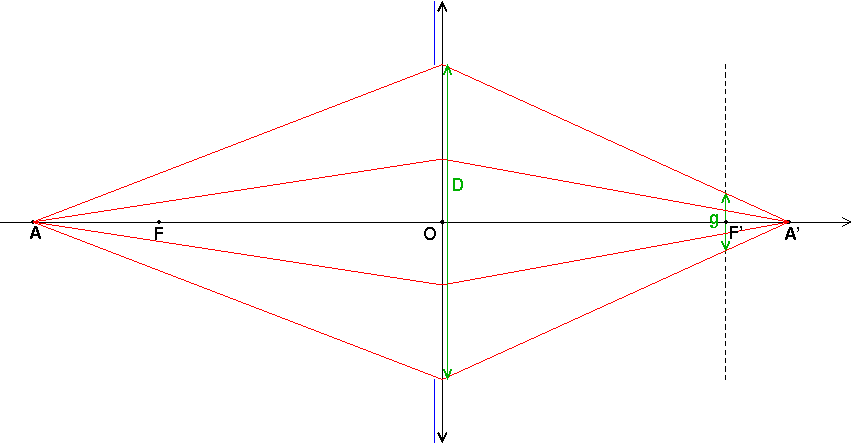
En fait j'ai un peu plus réfléchi et si je représente les rayons extrêmes passant juste au bord du diamètre j'obtiens la figure suivante. Le rayons du disque au niveau de l'objectif serait alors la distance que j'ai coloriée en vert ??
Woow ok au moins la c'est clair (joli schéma).
Donc d'après la relation de conjugaison j'ai soit
En appliquant Thalès j'ai :
soit
Et en remplaçant avec OA' trouvé juste avant :
et après simplification et tout le tralala :
Qu'en dites vous ?
Merci beaucoup pour votre suivi très attentionné !
OK pour la relation de conjugaison
Erreur dans l'application du théorème de Thalès ; selon moi :
Je te laisse corriger la suite en conséquence.
Certains de nos messages se sont croisés.. Tu n'as pas tenu compte de mon message de 20h51 et ton résultat n'est pas réaliste. En pratique : g<<D, ton résultat conduit donc à H à peine supérieur à f'. Connaissant les valeurs de f' pour les appareil photos bas de gamme n'ayant pas de réglage possible de la distance de O aux capteurs, il faut obtenir une valeur de H très supérieure à f'.
Il te faut reprendre mon message de 20h51...