Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths supForum Supérieur de maths sup PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths sup
Partager :

Optique

Posté par
QLglt27 30-09-17 à 15:44

Bonjour a tous j'ai un tout petit exo d'optique a faire et je bloque ...
Voici l'exo :
Un objet AB est conjugué de son image A'B' par une lentille convergente, dans les conditions de Gauss. Un rayon lumineux incident passe en A en faisant un angle avec l'axe optique,l'émergent correspondant est incliné d'un angle ' lorsqu'il passe en A'. On note g='/ le grossissement angulaire.

1) A l aide d'une construction géométrique, relier g et le grandissement transversal =A'B'/AB (algébriques)

2) Lorsque le système optique centré est constitué de plusieurs lentilles mises en cascade, peut-on encore obtenir une telle relation entre les tailles et les angles, dans des plans conjugués par le système entier ?

Pour la question 1 je vois tres bien qu'il y a deux triangles qui ont un coté en commun mais je trouve g=arctan (h/OA')/arctan(h/OA). Je narrive pas a trouver le lien avec le grandissement transversal

Pour la question 2 pouvez vous m'expliquer ce que signifie "dans des plans conjugués par le systeme entier"

Merci d avance

Posté par
QLglt27re : Optique 30-09-17 à 15:59

Alors petite rectification,  la question 1 c'est bon. En faite etant donné que nous sommes dans les conditions de Gauss, tan =. Donc cela mamène à  g=OA/OA'=AB/A'B'=1/

Pouvez vous donc seulement m'aider pour la question 2 svp

Posté par
QLglt27re : Optique 30-09-17 à 16:01

QLglt27 @ 30-09-2017 à 15:44

Bonjour a tous j'ai un tout petit exo d'optique a faire et je bloque ...
Voici l'exo :
Un objet AB est conjugué de son image A'B' par une lentille convergente, dans les conditions de Gauss. Un rayon lumineux incident passe en A en faisant un angle avec l'axe optique,l'émergent correspondant est incliné d'un angle ' lorsqu'il passe en A'. On note g='/ le grossissement angulaire.

1) A l aide d'une construction géométrique, relier g et le grandissement transversal =A'B'/AB (algébriques)

2) Lorsque le système optique centré est constitué de plusieurs lentilles mises en cascade, peut-on encore obtenir une telle relation entre les tailles et les angles, dans des plans conjugués par le système entier ?

Pour la question 1 je trouve  g=OA/OA'=AB/A'B'=1/

Pour la question 2 pouvez vous m'expliquer ce que signifie "dans des plans conjugués par le systeme entier"

Merci d avance

Posté par
QLglt27re : Optique 30-09-17 à 16:07

Désolé pour le dernier message je pensais que je pouvais modifer le message, en fin de compte cela me l'as simplement réenvoyé. Toutes mes excuses...

Posté par
Priamre : Optique 01-10-17 à 09:43

2) Tu pourrais consulter Google " Systèmes centrés optique ", spécialement  "ressources.univ lemans".

Posté par
QLglt27re : Optique 01-10-17 à 12:04

Merci Priam, Je viens de consulter le site il est très intéressant mais trop poussé par rapport à mon programme de physique.


La réponse à la question, je pense que c'est non mais comment le démontrer ??

Posté par
QLglt27re : Optique 02-10-17 à 12:29

Aidez moi svp

Posté par
vanoisere : Optique 02-10-17 à 14:19

Bonjour
Deux plans sont conjugués par un système optique lorsque, de tout point du premier plan, le système optique donne une image appartenant au second plan.
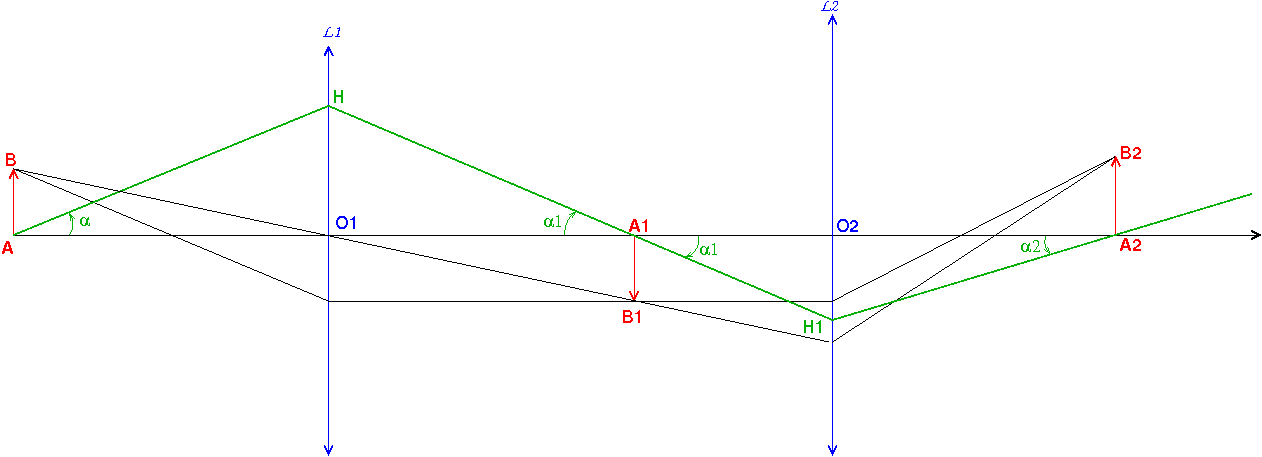
Regarde la figure ci-dessous.
Le plan orthogonal à l'axe optique contenant A et le plan orthogonal à l'axe optique contenant A1 sont conjugués par la lentille L1.
Le plan orthogonal à l'axe optique contenant A1 et le plan orthogonal à l'axe optique contenant A2 sont cnojugués par la lentille L2.
Le plan orthogonal à l'axe optique contenant A et le plan orthogonal à l'axe optique contenant A2 sont conjugués par le système constitué des deux lentilles.
J'algébrise les distances et les angles.
Considérer O1H comme hauteur commune aux triangles (AO1H) et (A1O1H) permet d'écrire, puisque les angles sont faibles dans les conditions de Gauss :

\gamma_{1}=\frac{\overline{O_{1}A_{1}}}{\overline{O_{1}A}}=\frac{\alpha}{\alpha_{1}}=\frac{1}{g_{1}}
Même raisonnement pour L2 en remarquant les angles "opposés par le sommet" en A1 :

\gamma_{2}=\frac{\overline{O_{2}A_{2}}}{\overline{O_{2}A_{1}}}=\frac{\alpha_{1}}{\alpha_{2}}=\frac{1}{g_{2}}
Pour le système global formé des deux lentilles en cascade :

\gamma_{1}=\frac{\overline{O_{1}A_{1}}}{\overline{O_{1}A}}=\frac{\alpha}{\alpha_{1}}=\frac{1}{g_{1}}

\gamma_{2}=\frac{\overline{O_{2}A_{2}}}{\overline{O_{2}A_{1}}}=\frac{\alpha_{1}}{\alpha_{2}}=\frac{1}{g_{2}}

\gamma=\frac{\overline{A_{2}B_{2}}}{\overline{AB}}=\frac{\overline{A_{2}B_{2}}}{\overline{A_{1}B_{1}}}\cdot\frac{\overline{A_{1}B_{1}}}{\overline{AB}}=\gamma_{1}\cdot\gamma_{2}

Le grandissement transversal de l'association de lentilles est le produit des grandissements transversaux de chacune des lentilles. Cela peut se généraliser à un nombre quelconque de lentilles minces en cascades :

\gamma=\prod_{i=1}^{n}\gamma_{i}

De la même façon :

g=\frac{\alpha_{1}}{\alpha}\cdot\frac{\alpha_{2}}{\alpha_{1}}=g_{1}\cdot g_{2}

Généralisation :

g=\prod_{i=1}^{n}g_{i}

Puisque, pour chaque lentille : g_{i}=\frac{1}{\gamma_{i}} , on obtient pour une association en cascades de lentilles minces de même axe optique :

\gamma=\frac{1}{g}

Optique

Posté par
QLglt27re : Optique 02-10-17 à 19:01

Franchement merci beaucoup d'avoir pris beaucoup de temps pour me répondre, tout est clair, c'est super bravo à vous

Je vous souhaite une bonne soirée et encore merci


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !