Bonsoir Kat !

je vois qu'on a abandonne les frottements pneu sur route pour attaquer les problemes de ces pauvres myopes (depuis le temps qu'on pose des sujets d'examens sur leur dos, on se demande pour quoi ils sont toujours malades !).
Bon, 1ere question : moi le punctum optimum je ne sais pas ce que c'est. Je devine que c'est le punctum proximum (cad le point le plus pres pouvant etre vu nettement, apres accommodation maximum), mais j'aimerais que te me le confirmes.

Apres, tu as raison : connaissant la position du Pp et la valeur de A, on peut calculer la position de son punctum remotum Pr, qui pour un myope n'est pas tres loin. Cela dit, il faudrait m'expliquer cette phrase "P-optimum = 54 dioptries", sachant que moi, je ne sais pas faire la correspondance entre un point et une puissance. (et d'ou vient ce nombre 54 dioptries qui ne figure pas dans l'enonce ?).

Enfin, je suppose que la correction doit ameliorer sa vision de loin, mais je ne comprends pas la phrase "après correction en avant de l'oeil". Va-t-il porter un verre correcteur (donc une paire de lunettes, a 1 ou 2 cm du centre optique de l'oeil, ou une lentille de contact plaquee sur ce centre optique ?

Bonsoir prbebo

C'est bien ça: punctum optimum = punctum proximum, c'est la même chose.

J'ai pris la valeur de 54 dioptries car c'est la puissance de l'oeil chez un sujet sain (soit une distance de 0.25 m) . J'ai dans mon cours une formule pour relier cette puissance et cette distance (notée Xp) : P-proximum = 1/xp + 1/0.02 .

Le sujet porte des lentilles je suppose, il n'y a pas de distance entre l'oeil et un possible verre de lunette indiquée.

OK, pour le punctum proximum j'avais devine ; mais l'appellation "optimum" ne figure dans aucun manuel. Donc, autant appeler un chat un chat...

Pour ta reponse a ma 2ieme remarque, il y a une contradiction : tu me dis que la puissance de l'oeil chez un sujet sain correspond a une distance minimale de vision distincte de 25 m, ce qui donne une puissance de 54 dioptries. Or, le debut de l'enonce precise bien que le sujet est myope... donc cette distance minimale de 25 cm n'a aucun sens pour lui (et pour moi non plus).

Je te signale aussi que la distance standard entre le centre optique de l'oeil et la retine est communement prise a 1,6 cm ; ca veut dire que si le sujet voit nettement a l'infini, le foyer image F' de son oeil se trouve a 16 mm du centre optique O, ce qui donne OF' = 16 mm = 1,6 x 10^-2 m et donc une convergence C_MIN = 1/OF' = 62,5 dioptries. S'il doit accommoder pour voir des objets rapproches, cette convergence va augmenter. Cad que la convergence d'un oeil peut difficilement tomber en-dessous de cette valeur, a moins que le sujet ne soit hypermetrope. Conclusion, un myope (dont l'oeil par definition est trop convergent) et qui en vision au punctum proximum a une convergence de 54 dioptries, moi ca me pose des problemes.

Il est tard et je te donne simplement le debut de la solution (cad, on ne parle pas encore des lentilles correctrices) :
J'appelle pour simplifier les notations D la distance maximale de vision distincte (cad la distane arithmetique entre le centre optique de l'oeil et son punctum remotum), et d la distance minimale de vision distincte (cad la distane arithmetique entre le centre optique de l'oeil et son punctum proximum). Dans le cas de l'exercice d vaut 10 cm et D est inconnu.
J'appelle aussi C_MIN la convergence minimale de l'oeil (cad quand il regarde a son p.r.), et C_MAX la convergence maximale (vision au p.p.).
D'ici demain, essaie de montrer que l'on a C_MAX - C_MIN = 1/d - 1/D (demo demain). Par definition, cette quantite C_MAX - C_MIN s'appelle amplitude dioptrique A.

Si on connait A et d, il est facile de calculer D. Moi je trouve D = 25 cm. Au-dela de cette distance, le sujet ne peut pas voir net.

En admettant qu'il va porter des lentilles de contact, la distance focale de cette lentille est facile a trouver. Dis-moi ce que tu en penses, je reprends l'ecoute demain vers 13 heurs.

BB.

Merci pour l'explication ; je pensais que seule la vision de loin d'un myope était modifiée ! (et je suis myope; honte sur moi ^^ )

Alors je pars des 2 formules : Cmax = 1/0.02 + 1/d et Cmin = 1/0.02 + 1/D.
Donc Cmax - Cmin = 1/0.02 + 1/D - (1/0.02 + 1/d); en soustrayant je trouve Cmax - Cmin = 1/d - 1/D.

Comme l'amplitude dioptrique A = Cmax - Cmin = 6, je fais le calcul en remplaçant d par 10 cm, donc D = 25 cm.

Je trouve ensuite Cmax = 1/0.02 + 1/0.25 = 54 D; il lui faut une correction de -4 D.
Puis , avec cette correction je recalcule d : -4 = 1/d - 1/0.1; je trouve d = 16.67 cm... j'espère qu'il n'y a pas d erreur avec les signes :s

Bonjour Kat,

bravo c'est bien ca : la distance focale de la lentille correctrice est bien f'_c = - 25 cm, donc une divergente, et le punctum proximum avec cette lentille recule et passe a 16,67 cm du centre optique de l'oeil (au lieu de 10 cm). Donc aucune erreur.
Moi aussi je suis myope, et chaque fois que j'explique a mes etudiants que la lentille correctrice, non seulement corrige la vision eloignee en renvoyant le PR a l'infini, mais encore fait reculer le PP et donc ameliore la vision de pres (on n'est plus oblige de tenir le journal a 10 cm de son nez), ca provoque un etonnement !

Cela dit, une remarque : je conteste un peu la relation C = 1/0.02 + 1/distance, car j'ai l'impression que le 1/0.02, qui correspond a une distance de 2 cm, represente la distance entre le centre optique de l'oeil et la retine (pour moi c'est beaucoup, 15 ou 16 mm sont plus raisonnables). Bien sur, si  c'est dans le cours il faut l'utiliser, d'autant plus que tu sais t'en servir et qu'elle te donne les bons resultats. Mais ma remarque est celle-ci : cette distance de 2 cm n'est pas necessaire pour traiter ce genre de problemes. Il y a une autre facon de raisonner, qui conduit au resultat sans passer par une formule toute faite.

Je t'explique rapidement, pour la recherche de la distance focale f'_c du verre correcteur :
a) l'oeil doit voir net sans accommodation,  donc les rayons sortant du verre correcteur doivent sembler provenir du PR (le vrai, celui de l'oeil malade) ;
b) il veut voir un objet situe a l'infini, donc les rayons entrant dans le verre correcteur forment un faisceau incident parallele a l'axe optique.
c) je rassemble ces deux infos : le verre correcteur, eclaire par un faisceau incident //, fait converger le faisceau vers son foyer image (virtuel ici) ; et puisque ce faisceau doit sembler provenir du PR, j'en conclus que le foyer image F'_c de la lentille correctrice doit etre place sur le PR de l'oeil myope, cad a 25 cm de l'oeil. On trouve immediatement la distance focale du verre : f'_c = - 25 cm, soit une puissance de -4 dioptries.  Aucun calcul la-dedans !

Puisque ton pb est fini, je vais m'occuper des autres questions posees sur le forum. Plus tard (cad das qqes jours) je te detaillerai, avec schemas, comment avec cette methode la position du nouveau PP apres correction.

A bientot, et bravo encore. BB.

D'accord, merci beaucoup !

Bonjour Kat !

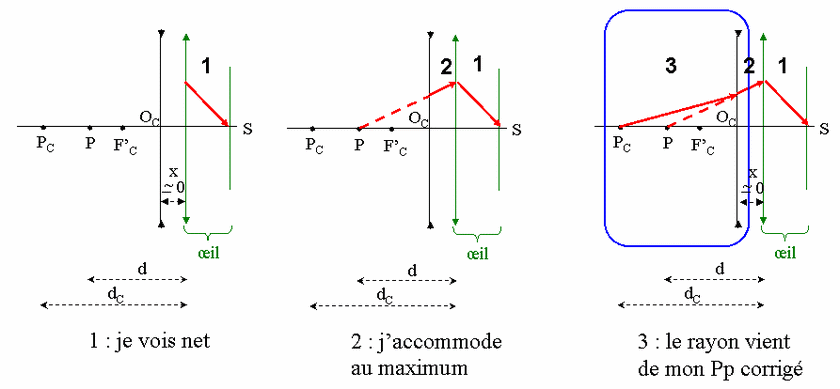
Chose promise, chose due. Voici comment j'explique la correction de la vision rapprochee pour un myope. Vois sur le schema ci-dessous les notations employees : j'appelle P le punctum proximum de l'oeil myope, P_C le punctum procimum apres correction, O_C et F'_C le centre optique et le foyer image de la lentille correctrice (divergente bien sur). L'oeil est ramene a la lentille equivalente (cornee + cristallin) et a la retine qui coupe l'axe optique en S (parce que je  garde la lettre R pour le punctum remotum...). Les distances arithmetiques sont indiquees en-dessous : d, distance entre le PP non corrige et le centre optique de l'oeil, d_C celle entre le PP corrige et l'oeil ; la distance separant le verre correcteur de l'oeil est notee x. Meme quand elle est supposee nulle, il faut la faire figurer sur le schema en ecartant legerement la lentille de l'oeil. La distance separant la retine du centre optique de l'oeil n'est pas baptisee, car on n'en a jamais besoin.

Maintenant, l'astuce consiste a tracer la marche du rayon lumineux en partant de la fin, c'est a dire depuis son arrivee sur la retine, pour remonter progressivement vers la source (ici le P_C). Cette construction se fait en trois etapes :
Etape 1 : l'oeil voit nettement un point situe quelque part sur son axe optique : donc les rayons issus ce ce point viennent focaliser en S.
Etape 2 : l'oeil accommode au maximum (puisqu'il cherche a ajuster sa vision rapprochee). Donc le rayon qui arrive en S semble provenir du punctum proximum P de l'oeil. On trace donc le rayon incident sur l'oeil en l'alignant avec P. Ce rayon est aussi celui qui est sorti de la lentille correctrice.
Etape 3 : L'emergent de l'etape 2 correspond a un rayon incident qui est venu de P_C. La construction montre bien que P_C est necessairement eloigne  de l'oeil, puisque le verre correcteur est divergent.

Maintenant, on regarde dans la bulle bleue du 3ieme schema, qui englobe ce qui s'est passe au niveau de la lentille correctrice : l'objet qui l'eclaire est P_C, et elle en donne une image placee en P. Il ne reste donc plus qu'a ecrire l'equation de conjugaison :
-1/ + 1/ = 1/,
dans laquelle la distance arithmetique O_CP_C vaut d_C-x, c'est ce que l'on cherche, la distance arithmetique O_CP vaut d-x, connue, et ou vaut f'_C, distance focale du verre correcteur, negative, connue aussi puisqu'on l'a choisie pour corriger la vision eloignee. Bien entendu, si le verre correcteur est une lentille de contact, x est nul  et ce sont les distances d et d_C qui interviennent dans l'equation de conjugaison.Il faut juste faire attention aux signes, puisque , et f'_C sont negatives.

Et je n'ai pas besoin de savoir si la retine est a 15, 16 ou 20 mm du cristallin : cette grandeur, qui figure dans ta formule "toute faite", n'intervient en realite pas dans le calcul.

Voia, j'espere que tu as tout compris !   B.B.

Bonjour prbebo

Je comprends bien de cette façon oui, les schémas aident beaucoup ! En cours je vois juste toutes les formules à appliquer avec la distance de 2 mm..

Un grand merci pour avoir consacré un peu de temps sur ce problème

Bonsoir Kat,

2 cm et non 2 mm, c'est la distance qui separe la retine du centre optique de l'oeil reduit. Mais ce n'est pas grave, l'essentiel est que tu aies compris qu'un raisonnement, surtout expose a l'aide de schemas, est infiniment preferable a l'usage d'une formule toute faite, et dont on ne connait pas toujours les limites.
Au plaisir de te retrouver pour d'autres challenges en optique (quoique  cette annee universitaire se termine bientot).  BB.