Inscription / Connexion Nouveau Sujet
Ondes progressive sinusoïdale en sin²
Bonjour,
Travaillant actuellement sur un exercice sur les ondes progressives, je suis face à une difficulté.
On considère une impulsion décrite par la fonction y(x, t=0)= A0 sin2(x) qui se propage dans le sens des x croissants et avec x entre 0 et 
.
Je cherche à exprimer y(x,t) à un instant t.
J'exprime la fonction sous la forme classique y(x,t)=A cos (
t - kx + 
).
J'obtiens ainsi l'expression : y(x,t) = A cos ((t-(x/c)).
Comme il n'y a qu'un seul signal, on peut considérer nul. Ou ai-je mal compris ?
En considérant l'expression en t=0, je peux écrire l'égalité en remplacement t par 0 dans ma dernière expression.
Ensuite, ce carré pour le sinus me bloque. Y a-t-il une relation trigonométrique pour simplifier cela ?
Merci pour vos réponses,
Bonjour
J'ai représenté en rouge y(0,x). On considère que le signal se propage dans le sens des x positif à la célérité c sans amortissement. Entre la date zéro et la date t quelconque, le signal se propage donc sans se déformer de la distance (c.t). On peut considérer que la valeur de y à un instant de date t quelconque et à une abscisse x est la valeur de y qui existait à la date zéro et à l'abscisse (x-ct). Tu obtiens donc, à la date t quelconque :
y(t,x)=A.sin2(x-ct) pour (x-c.t) compris entre zéro et (unité arbitraire non précisée).
Pour résumer :
x<c.t : y=0
c.t
xc.t+ : y(t,x)=A.sin2(x-ct)
x>c.t+ : y=0
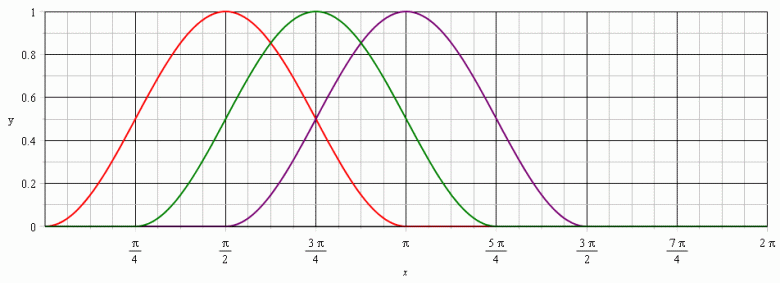
Pour illustrer cela, voici trois courbes représentant (en rouge) y=f(x) pour t=0, en vert, y=g(x) pour c.t=/4, en violet, y=h(x) pour c.t=/2.
On visualise bien la propagation du signal dans le sens positif à la célérité c. J'ai posé arbitrairement : A=1 (unité inconnue)
Bonjour,
Merci pour la réponse à mon message!
Cela me semble si simple en le lisant. J'avais commencé en écrivant y(t,x)=A.sin2(x-ct) pour (x-c.t) compris entre zéro et et puis je me suis dit qu'il fallait poursuivre le calcul après avoir vu sur internet des exemples où la fonction y(x,t) était décrite par des exponentielles et d'autres fonctions sinusoïdales.
Il n'est pas donc pas nécessaire d'écrire une égalité avec la forme générale pour exprimer y(x,t) tant que l'on fait le lien entre y(x,t) et y(x-ct,0) ?
Par ailleurs, puisque le signal se propage sans amortissement, on peut écrire directement A0=A, non?
Par rapport au schéma d'illustration, en effet, on visualise bien la propagation du signal.
Mais si je considère que x est compris entre 0 et , cela ne signifie-t-il pas qu'à partir de l'abscisse x=, la fonction y(x,t) sera nulle (les courbes vertes et violettes "revenant" subitement à zéro à partir de cette abscisse) ?
Il n'est pas donc pas nécessaire d'écrire une égalité avec la forme générale pour exprimer y(x,t)
Les trois lignes du message précédent en caractère gras résument la situation générale à chaque instant.
Concernant ton dernier paragraphe : le signal concerne la portion d'espace x
[0,] seulement à la date t=0. A une date t quelconque, la déformation affecte toujours une "longueur" égale à mais, comme cette perturbation se propage la la célérité c, la portion d'espace affectée par la perturbation correspond à x[c.t , c.t + ].
Si tu ne te représentes pas bien la situation physique, tu peux réaliser (ou à défaut imaginer) l'expérience suivante. Tu poses sur le sol une longue corde (une dizaine de mètres) assez lourde et assez souple. Avec une main, tu soulèves une extrémité rapidement de quelques dizaines de centimètres et reposes cette extrémité au sol. Tu as ainsi produit une déformation de la corde ayant approximativement l'allure étudiée ici. Tu constates alors que cette déformation se propage le long de la corde ; chaque point de la corde se soulève verticalement au passage de la perturbation pour reprendre ensuite sa position d'équilibre au sol. En pratique, il y a amortissement du signal, phénomène qui est négligé ici.
A ce propos : tu as raison : on peut poser A=Ao dans ton exercice.
Annuler
connectez vous