Inscription / Connexion Nouveau Sujet
ondes et dispersion
Bonjour à tous,
J'ai un exercice de niveau L2 physique que je n'arrive pas à faire entièrement. Voici l'énoncé :
1. Soit une onde monochromatique qui s'écrit :
avec le vecteur d'onde.
a) Rappeler la définition d'un front d'onde (ou une surface d'onde).
-- fait, une surface d'onde est une surface sur laquelle la fonction d'onde est uniforme, càd. a la même valeur partout sur la surface, à un instant "t" donné.
b) Montrer que les fronts d'onde sont des surfaces en tout point perpendiculaire à la direction de propagation de l'onde (vous pourrez considérer l'instant t = 0).
-- je ne suis pas certain de ce que j'ai fait ici, je prend t=0 donc , et je dis "or
est l'amplitude de l'onde à t=0, donc
donc les vecteurs k et k sont perpendiculaires... mais je ne vois pas bien ce qu'est le vecteur
finalement donc ça ne fait aucun sens physique pour moi, je ne comprend pas.
2. Lors de la propagation unidimensionnelle d'une onde acoustique dans un fluide (de l'eau par
exemple), la pression est décrite par une fonction
et la relation de dispersion est :
Dans cette équation, est la vitesse de l'onde sans atténuation, et
est un temps caractéristique qui dépend de la viscosité du liquide
et de la masse volumique
:
a) Calculer l'ordre de grandeur de la quantité pour une onde ultrasonore de fréquence
1 MHz. On prendra c = 1500 m·s-1 et η = Pa·s.
-- J'ai faut un binôme du second degré et j'ai une expression de très lourde, avec
b) Ecrire la relation de dispersion. En utilisant une approximation justifiée par la question a),
écrire cette relation sous la forme k = kr(ω) + j ki(ω).
-- la relation de dispersion est
c) En déduire que la pression peut s'écrire sous la forme :
où L est une distance caractéristique d'atténuation. Calculer cette longueur d'atténuation L pour
des fréquences de 1 MHz, 10 MHz et 100 MHz.
Merci d'avance pour votre aide
Bonjour
Pour 1.a) : que signifie pour toi : " fonction d'onde uniforme" ?
D'accord pour 1.b)
Pour 2 : il faut bien faire la différence, y compris dans les notations, entre la pression acoustique p(x,t) et le complexe associé qu'il vaudrait mieux noter p(x,t) .
Qu'est-ce qui te gêne exactement ? As-tu des questions précises à poser ?
Bonjour
Pour 1.a) : que signifie pour toi : " fonction d'onde uniforme" ?
Bonjour,
Cela signifie que la fonction d'onde a la même valeur en tout point de la surface d'onde (valeur scalaire) pour un instant "t" donné. C'est dans mon cours, uniforme signifie "même valeur pour un instant donné", et constant signifie "même valeur peu importe l'instant". En gros uniforme représente une constance "en fonction de l'espace" (peu importe l'espace la valeur est la même) et constant représenterait une constance "en fonction du temps" (peu importe le temps la valeur reste la même). En tout cas c'est ce que j'ai compris, je peux me tromper.
D'accord pour 1.b)
Pour 2 : il faut bien faire la différence, y compris dans les notations, entre la pression acoustique p(x,t) et le complexe associé qu'il vaudrait mieux noter p(x,t) .
Qu'est-ce qui te gêne exactement ? As-tu des questions précises à poser ?
Désolé je n'ai pas été assez clair, en fait la 2.a) et 2.b) je n'arrive pas.
Pour 2.a) je réécris l'expression ainsi pour avoir le binôme :
et la résolution :
Ca ne m'avance pas beaucoup car la question est "Calculer l'ordre de grandeur de la quantité
En y repensant peut-être que finalement je dois juste utiliser la relation

Pour la 2.b), j'ai la relation de dispersion
Les surfaces d'onde sont les lieux des points M de l'espace tels que la pression acoustique soit la même à chaque instant. Cela implique ici : : vecteur constant, pas nécessairement le vecteur nul comme tu l'as écrit. Si on s'intéresse à un point H quelconque de la droite passant par O et dirigée par le vecteur
: si M appartient à un plan perpendiculaire à cette droite et passant par H, on a bien :
. Les surfaces d'onde sont donc les plans perpendiculaires à la direction de propagation qui est la direction du vecteur
. Pour cette raison, on parle d'onde plane.
Pour la question 2 : l'application numérique demandée conduit à . Alors ,en notation complexes :
En supposant la propagation dans le sens positif :
(développement limité...)
Ne pas oublier pour bien comprendre l'intérêt du problème que l'absence d'amortissement conduirait à : .
Les surfaces d'onde sont les lieux des points M de l'espace tels que la pression acoustique soit la même à chaque instant. Cela implique ici :
Désolé mais je ne comprend pas, M appartient à la surface d'onde, et H aussi ? Je ne comprend pas à quoi sert H... pour avoir des choses perpendiculaires il faut bien qu'un produit scalaire soit nul à un moment non ?
Pour la question 2 : l'application numérique demandée conduit à
En supposant la propagation dans le sens positif :
Ne pas oublier pour bien comprendre l'intérêt du problème que l'absence d'amortissement conduirait à :
D'accord je vois mieux cette partie, en fait je remplaçais
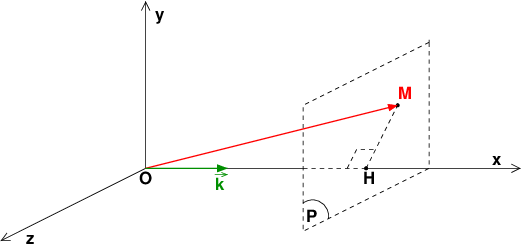
Ton premier raisonnement supposant concerne le plan d'onde (Oyz) mais ce n'est pas le seul plan d'onde possible. Tout plan (P) perpendiculaire au vecteur
donc perpendiculaire à l'axe (Ox) est un plan d'onde. Soit M un point quelconque de ce plan et H son projeté orthogonal sur l'axe (Ox) : voir figure.
Propriété élémentaire du produit scalaire :
Quel que soit M appartenant à (P) :
si x désigne l'abscisse du point M.
A un instant donné, la phase de l'onde est donc la même pour tous les points M d'un même plan perpendiculaire au vecteur .
Ton premier raisonnement supposant
Propriété élémentaire du produit scalaire :
Quel que soit M appartenant à (P) :
si x désigne l'abscisse du point M.
A un instant donné, la phase de l'onde est donc la même pour tous les points M d'un même plan perpendiculaire au vecteur

Donc pour tout point M de n'importe quel plan orthogonal à
Pour la 2.c), je trouve
OK pour les plans d'onde. Cela revient à dire que dans n'importe quel plan perpendiculaire à la direction de propagation, la pression acoustique à un instant donné est la même en tout point de ce plan.
Attention au signe ! En imaginant une onde sa propageant dans le sens positif de l'axe (Ox), la valeur instantanée de la pression acoustique est la partie réelle du complexe associé :
avec :
Il faut obtenir L>0 : cela correspond à une onde plane qui se propage à la célérité ca avec amortissement : son amplitude diminue exponentiellement en fonction de la distance parcourue.



