Inscription / Connexion Nouveau Sujet
Ondes : corps en oscillation
Bonjour l'ile !
J'ai besoin de votre aide SVP :
Voici mon sujet :
La position initiale d'un corps en oscillation est de 3 cm. La fréquence de l'oscillation est de 0,2 Hz.
L'amplitude du mouvement oscillant est de 5 cm.
1. Quelle est la constante de phase des oscillations ?
2. Quelle est la pulsation de l'oscillation ?
3. Quelle est la valeur de la vitesse maximale ?
4. Quelle est la valeur de l'accélération maximale ?
pour la question 2 j'ai trouvé 2pi/5 rad/s ensusite les autres questions je n'arrive pas à trouver
***Edit gbm : niveau mis en accord avec ton profil***
Bonsoir,
Je crois que ton énoncé est incomplet : puisque l'abscisse initiale a une valeur absolue différente de l'amplitude, il faut supposer que la vitesse initiale est non nulle. Pour résoudre correctement le problème, il faudrait savoir si cette vitesse initiale est positive ou négative...
Ne peut-on pas déduire la vitesse initiale ?
En effet si le déplacement est donné
Alors au temps t=0 si D = 3 et A = 5, alors la valeur de s'en déduit.
Mais d'autre part, de la relation entre vitesse V et déplacement
au temps t = 0, puisque est connue, de même que A et
, il est a priori possible de déterminer une unique valeur pour la vitesse au temps t=0.
Je ne vois pas à quelle ambiguïté précisément vous faites allusion.
Bonsoir,
En effet si le déplacement est donné D=A\cos (\omega t + \Phi)
Alors au temps t=0 si D = 3 et A = 5, alors la valeur de \Phi s'en déduit.
La condition initiale conduit à :
Cela conduit à deux solutions possibles :
0,927rad et -0,927rad.
Pour lever l'ambiguïté, il faut raisonner sur la vitesse :
L'amplitude A étant positive ainsi que la pulsation
, le signe de la vitesse à la date t = 0 est donc le signe de - sin().
Conclusion :
L'énoncé est donc bien incomplet !
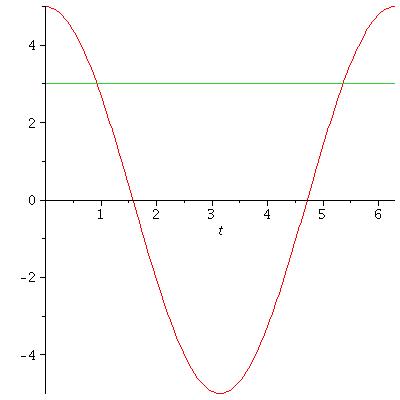
Une illustration graphique de mon message précédent ; en rouge : la courbe D=f(t) d'amplitude 5cm représentée sur une période (origine des temps arbitraire). On voit bien que l'abscisse D = 3cm correspond, par période, à deux situations physiquement différentes : une situation où la vitesse est négative, une situation où la vitesse est positive.
Bonsoir,
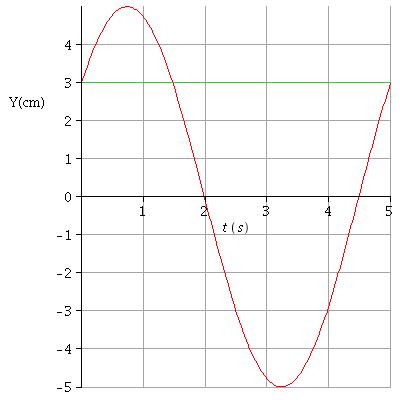
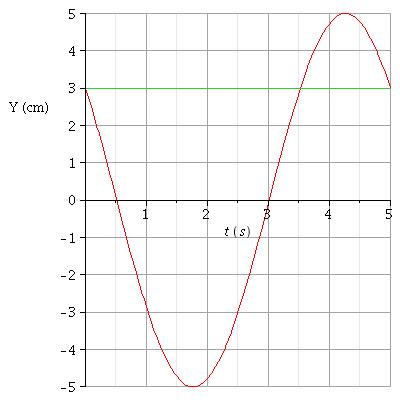
En espérant que cela pourra aider lolo77150, voici les deux courbes représentant les variations en fonction du temps de l'ordonnée Y du point en mouvement pour les deux situations possibles du problème. Dans le premier cas, la vitesse initiale est positive, dans le second cas, la vitesse initiale est négative.
Remarque : la phrase : "La position initiale d'un corps en oscillation est de 3 cm" est erronée. Je l'ai traduite par : "l'ordonnée initiale est 3cm".
Annuler
connectez vous