Inscription / Connexion Nouveau Sujet
Océan et réchauffement climatique
Bonjour,
J'ai besoin d'aide pour un exercice d'enseignement scientifique. J'ai l'impression qu'il manque des informations dans les documents. Ou bien je ne comprends pas les documents.
Voici l'énoncé :
On observe avec le réchauffement climatique une augmentation du niveau marin d'environ 18 cm depuis 1900. Pour certains individus l'augmentation du niveau marin serait actuellement due essentiellement à la dilatation thermique des eaux océaniques, d'autres affirment qu'elle est le résultat de la fonte des glaces.
On cherche à déterminer la validité de ces affirmations.
1. En supposant que la surface des océans reste constante, calculer la hausse du niveau des océans par dilatation thermique depuis 1900 (augmentation de température de 0,6°).
2. Sachant que la surface des océans est estimée à 360.106 km², déterminer la hausse du niveau marin due à la fonte des glaces continentales depuis 1960.
3. Déterminer la hausse du niveau marin que provoquerait la fonte de la totalité des glaces continentales.
4. Répondre au problème posé.
Voici ce que j'ai fait jusqu'à maintenant :
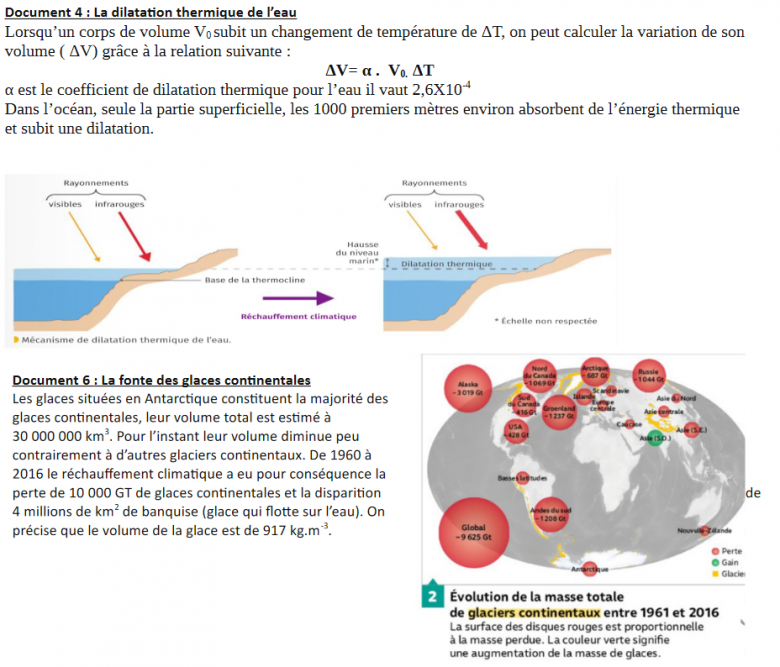
1. Avec la formule du document : ΔV=α.V_0.ΔT = 2,6*10^(-4)*V_0*0,6
je ne sais pas quelle valeur écrire pour V_0.
2. Ici, comme pour la question 1, j'ai l'impression qu'il manque des informations, je n'arrive pas à répondre.
3. Même souci que pour la question 2.
4. Je ne comprends pas la question.
J'ai besoin d'aide pour pouvoir clarifier tout ça.
Merci !
Bonjour
Il faut s'intéresser à une couche d'eau de hauteur initiale ho=1000m et d'aire de surface S quelconque. Le volume initial est ainsi Vo=ho.S
L'augmentation de volume s'écrit ainsi  V=S.
V=S. h
h
où  h est la hausse recherchée...
h est la hausse recherchée...
Je reprends la question 1 :
1. V_0 = h_0 * S = 1000*360*10^6 = 3.06*10^11 km^3 -> Je ne suis pas sûr de l'unité.
Cela correspond au volume d'eau qui subit une dilatation.
ΔV=α.V_0.ΔT = 2,6*10^(-4)*3.06*10^11*0,6 = 47736 km^3
Le volume de l'océan a augmenté de 47736 km^3 par dilatation thermique.
ΔV=S.Δh ⇔ Δh = ΔV/S = 47736/3.06*10^11 = 1.326*10^-4 km = 13.26 cm
Le niveau des océans s'est élevé de 13.26 cm depuis 1900.
Il doit y avoir des erreurs dans ce que j'ai fait...
Commence par raisonner littéralement. Tu vas constater que l'aire S se simplifie et disparaît de l'expression de  h.
h.
On a ΔV=α.V_0.ΔT et ΔV=S.Δh
donc Δh*S = α*V_0*ΔT ⇔ Δh*S = α*h_0*S*ΔT ⇔ (Δh*S)/S = α*h_0*ΔT ⇔ Δh = α*h_0*ΔT
Il y a une erreur dans ce que j'ai envoyé pour la question 2 : la surface des océans est estimée à 360*10^6 km², et non 360,106 km².
Et il y a deux questions que je n'ai pas envoyées :
- Déterminer la contribution de la banquise (sur la mer) et des glaces continentales à l'élévation du niveau des mers
- Récapituler sous forme d'un schéma les interactions climat océan mises en évidence
Pour le schéma, ça va être difficile d'expliquer ce que j'ai fait, à moins d'envoyer un dessin... Mais bon je n'en suis pas encore là.
Je me répète : S disparaît du calcul par simplification ; tu n'as donc pas à calculer Vo. Il te suffit d'utiliser la formule démontrée dans ton message du 03-03-21 à 21:54 :
 h=
h= .ho.
.ho. T
T
 mesuré en °C-1 (unité oubliée dans ton énoncé...)
mesuré en °C-1 (unité oubliée dans ton énoncé...)
 T mesuré en °C
T mesuré en °C
 h mesurée avec la même unité que ho.
h mesurée avec la même unité que ho.
Or : ho = 1000m
Pour la question 2 : on connait la masse de glace continentale qui a fondue : dix mille gigatonnes. La fusion modifie le volume mais ne modifie pas la masse. La masse d'eau dans les océans a donc augmenté de dix mille gigatonnes. Quel est l'augmentation de volume des océans dû à ce phénomène ? En notant  V1 cette augmentation de volume et S l'aire de la surface des océans, quelle est la hausse de niveau correspondante, notée
V1 cette augmentation de volume et S l'aire de la surface des océans, quelle est la hausse de niveau correspondante, notée  h1 ?
h1 ?
Remarque : le document parle aussi des banquises qui sont des glaces flottantes.
Question : la fusion d'un iceberg fait-elle augmenter le niveau des océans ? Il existe une démonstration précise pour obtenir la réponse ; elle utilise le théorème d'Archimède. A défaut, tu peux réaliser chez toi une expérience très simple : dans un verre assez large, tu places quelques glaçons et tu remplis le verre d'eau à raz bord. Attention : il ne faut pas mettre trop de glaçons car tous les glaçons doivent flotter. Laisse passer quelques heures pour que toute la glace ait le temps de fondre... L'eau déborde-t-elle du verre ? Que peut-on dire de l'évolution du niveau de l'eau lors de la fusion de la glace ?
1. Je trouve Δh = 2,6*10^(-4)*1000*0,6 = 0,156 m = 15,6 cm
2. La fonte des glaces continentales impacte le niveau des mer, mais pas la fonte de la banquise.
Pour l'eau : 1 kg = 1L donc 10 000 GT = 1 000*10^9 kL
Avec la formule de la question 1 :
Δh₁ = V₁ / S = (1 000*10^9)/(360*10⁶) = environ 2778 m... Ça me paraît beaucoup.
Il serait préférable de laisser la masse exprimée en tonnes car une masse d'eau (liquide) d'une tonne occupe un volume de 1m3.
Erreur dans ton énoncé : le symbole de l'unité "gigatonne" est Gt et non GT... le symbole de l'unité "tonne" est un "t" minuscule car ce nom ne dérive pas du nom d'un scientifique, contrairement au newton par exemple (symbole N).
Pour l'eau, 1t = 1m^3 donc 10 000 Gt = 10 000 *10^9 m^3
(10 000*10^9*10^-3)/(360*10^6) = 1/36 m soit environ 3 cm
Merci, je passe à la suite :
4. On V_2 = 30 000 000 km^3
h_2 = V_2 / S = 30 000 000 / (360*10^6) = environ 8,3 cm
Si la totalité des glaces continentales fondaient, la hausse du niveau de la mer serait de 8.3 cm.
Ici j'ai compté que les glaces continentales de l'arctique, faut-il que j'ajoute le résultat de la question précédente ?
Il faut tenir compte du fait que le volume de la glace n'est pas égal au volume de liquide pour une masse donnée. Tu peut commencer par déterminer la masse totale de glace continentale puis procéder comme à la question précédente.
Je n'arrive pas à calculer la masse de glace en utilisant les données de l'énoncé, je tombe sur des résultats inférieurs à 10 000 Gt ; pourtant dans l'énoncé, il est mentionné que les glaces de l'antarctique constituent la majorité des glaces continentales.
Pour trouver la masse des glaciers continentaux de l'antarctique, j'utilise la masse volumique :
30 000 000 km^3 = 30*10^9 m^3
d'après l'énoncé, la masse volumique de la glace vaut 917 kg.m^3
donc la masse de glace vaut 917*30*10^9 = 2,751*10*13 kg ce qui est inférieur à 10 000Gt
En cas de difficultés dans la conversation des unités, je conseille l'usage systématique des unités fondamentales du système international : masse en kg et volume en m3.
Tu n'as pas compris mon message du 04-03-21 à 14:21 concernant la question 2 ni mon message du 04-03-21 à 20:19. Lors de la fusion de la glace, la masse reste fixe mais le volume change ! Il faut faire intervenir la masse volumique de la glace. Il faut donc procéder comme je te l'ai indiqué précédemment.
Oui : puisque :
1km=103m
1km3=109m3
Reprend donc le calcul du volume de glace continentale en tenant compte de ce résultat et propose un calcul précis permettant d'obtenir la hausse du niveau des océans due à la fonte de toute cette glace.
Volume glaces continentales Arctique : 30 000 000 km^3 = 30 000 000*10^9 m^3
Masse volumique de la glace = 917 kg.m^3 donc masse de glace = 917*30 000 000*10^9 = environ 2.8*10^19 kg
Pour l'eau : 1t = 1m^3
2.8*10^19 kg = 2.8*10^16 t = 2.8*10^16 m^3
Volume glaces continentales qui ont fondu d'après la question précédente : 10 000 *10^9 m^3 d'eau
Volume total : 2.8*10^16 + 10 000 *10^9 = 2.801*10^16
Hausse du niveau marin : h = V / S = (2.801*10^16)/(360*10^6)
D'accord avec ton volume d'eau formé et d'accord avec ta méthode de calcul de h mais là encore : problème de conversion d'unité :
si 1km=103m, 1km2 = ... m2 ???
Oui ! Petit conseil : tu as intérêt ici à utiliser les puissances de dix pour améliorer la lisibilité.
Hausse du niveau marin : h = V / S
S = 360 * 10^6 km² = 360 * 10^6 * 10^6 = 360 * 10^12 m²
h = (2.801*10^16) / (360 * 10^12) = 92 mm -> Je ne suis pas sûr pour l'unité.
Diviser un volume mesuré en m3 par l'aire d'une surface mesurée en m2 conduit à une hauteur mesurée en mètre... En dehors de l'unité qui est fausse, je vois pas d'où sort ce "92"... Tu as vraiment de gros problèmes de gestion des unités...
Il faut aussi réfléchir au réalisme des résultats proposés. La masse de glace continentale est beaucoup plus élevée que la masse de glace ayant fondue depuis 1960. Il faut donc s'attendre à obtenir une augmentation du niveau beaucoup plus grande...
D'accord. Inutile d'insister je crois sur le caractère catastrophique pour l'humanité que représenterait la fonte de la totalité des glaces continentales...


