Niveau maths sup

notation complexe... beaucoup de mal!

Posté par
polka-dots 05-12-09 à 22:20

Bonsoir, ayant du mal avec la notion du régime sinusoïdal forcé, j'aimerais savoir pourquoi si on a:

\bar{u(t)}= E0exp(jwt)/1+w (trouvé grâce à la loi des mailles, dans un circuit RC), le module de \bar{u(t)} vaut: U= |E0exp(jwt)|/|1+w| = E0/ (1+jw) ?

De même je ne comprends pas pourquoi pour trouver le déphasage par rapport à e(t), on a:

= Arg(E0)-Arg(1+jw) = -Arg(1+jw).

Pourquoi pour calculer le déphasage, il faut faire l'argument de U?

Pourriez-vous mettre les étapes intermédiaires? J'ai vraiment du mal.

Pourquoi tan= - Im(1+jw)/Re(jw)= -w ?

Aidez-moi!! merci

Posté par re : notation complexe... beaucoup de mal! 05-12-09 à 23:19

A vrai dire je ne comprends pas le déphasage, c'est tout!

Posté par re : notation complexe... beaucoup de mal! 06-12-09 à 10:47

Il me semble que ton message est bourré de fautes.

bar{u(t)} = E0.exp(jwt)/ $\red{(}$ 1+ $\red{j}$ .Tau.w $\red{)}$ (trouvé grâce à la loi des mailles, dans un circuit RC), le module de \bar{u(t)} vaut: U= |E0exp(jwt)|/|1+ $\red{j}$ .tau.w| = E0/V(1+ $\red{(}$ tau.w $\red{)^2}$ ) ?

Il manque ensuite l'expression de e(t) que je suppose être:
$\red{e(t) = 1.e^{(jwt)}}$

on a alors bar{u(t)} / e(t) = E0./ $\red{(}$ 1+ $\red{j}$ .Tau.w $\red{)}$
-----

Lorsque un nombre complexe z est le rapport de 2 autres nombres complexes z1 et z2, soit z = z1/z2

alors |z| = |z1|/|z2|
et arg'z) = arg'z1) - arg(z2)

Et donc ici :
arg(bar{u(t)} / e(t)) = arg(Eo) - arg(1 + j.w.tau)

Et comme Eo est un réel, arg(Eo) = 0
---> arg(bar{u(t)} / e(t)) = - arg(1 + j.w.tau)

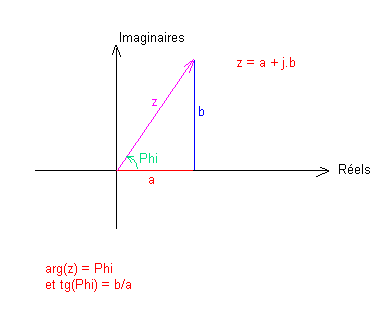
notation complexe... beaucoup de mal!

Sauf distraction.