Niveau maths spé

Nappe cylindrique

Posté par
EvDavid 13-01-18 à 17:44

Bonsoir,

Je travaillais un exercice qui porte sur une utilisation du potentiel vecteur, une partie qui n'est pas très détaillée dans le programme d'ailleurs. Seulement, je ne sais si c'est des lacunes du cours, ou une méthode de travail particulière qui est mise en application, mais je trouve des difficultés avec l'exercice. J'espère que vous pourrez m'aider afin que je puisse mieux maitriser cette notion de potentiel vecteur.

Un cylindre infiniment long d'axe Oz et de rayon R est parcouru dans le sens de sa longueur par un courant surfacique de densité non uniforme $\vec{j_{s}}=Msin(\theta )\vec{u_{z}}$ où M est une constante et l'angle en coordonnées cylindriques orienté à partir de l'axe Ox.
Après calcul on trouve que le champ sur l'axe Oz du cylindre est : $\vec{B(M)}=\frac{\mu _{0}M}{2}\vec{u_{z}}$ .
L'exercice a pour but de montrer qu'en réalité le champ magnétique est uniforme dans tout l'intérieur du cylindre. Pour cela on doit passer par le potentiel vecteur. Les question proposées sont :
1) Ecrire l'équation de Poisson pour le potentiel vecteur $\vec{A}$ en un point quelconque, intérieur ou extérieur au cylindre et justifier pourquoi il est de la forme $\vec{A}=A(r,\theta )\vec{u_{z}}$
=> En un point intérieur ou en dehors du cylindre on a pas de courant ( car distribution surfacique ) donc $\Delta \vec{A}=\vec{0}$ , et puisque Oz axe de révolution et distribution invariante par translation suivant Oz alors on a $\vec{A}=A(r,\theta )\vec{u_{z}}$
2) Chercher une solution en variables séparées $A(r,\theta )=f(r)g(\theta )$ ; après avoir trouvé une solution simple en $g(\theta )$ , explorer une solution pour $f(r)$ en $r^{p}$
J'aimerai bien savoir pourquoi on chercher des solutions de cette façon. Je veux dire, y'a-t-il un théorème physique ou des conditions de cette distribution qui nous permette de prendre des solutions en variables séparées ?
Bon je fais le calcul, l'équation de Poisson donne : $\frac{1}{r}\frac{\partial (rf')}{\partial r}$ $=-\frac{g''}{g}$ , un terme ne dépend que de r et l'autre que de on peut donc dire que les deux termes sont constants.

Dans le corrigé il est dit que g est 2-périodique et impaire en par anti-symétrie de la densité de courant, la solution $g(\theta )=\beta sin(\theta )$ conduit à cte=1
La restriction de sous la forme $f(r)=ar^{p}$ conduit alors à deux valeurs p=1 ou p=-1 . D'où la solution : $\vec{A(r,\theta )}=(ar+\frac{b}{r})sin\theta \vec{u_{z}}$

Je ne comprends pas pourquoi g doit vérifier ces conditions, ca doit, comme l'explique le corrigé, être lié à la distribution de courants, mais je ne vois pas trop pourquoi. Rien dans le cours ne nous impose, déjà une forme à variables séparées, ni des conditions sur chacune de ces fonctions.

J'espèer que vous pourrez m'aider afin de mieux comprendre ces manipulations sur le potentiel vecteur.

Merci d'avance.

Posté par re : Nappe cylindrique 14-01-18 à 19:33

Bonsoir
Remarque générale : pour éviter que certain problèmes de physique ne se transforment en purs problèmes de mathématique consistant à résoudre des équations différentielles, il est fréquent que les concepteurs essaient de faire "deviner" le type de solution par des raisonnement purement physique : étude des symétries, des invariances, des extremum...
Partant ici de l'expression générale de A(r,), il est assez facile de montrer sans calculs que A =0 pour =0 et pour =rad, que A présente, à r fixe, un maximum pour =/2 rad et un minimum pour =-/2rad. D'où la tentation "d'essayer" comme solution sin(). Evidemment, par cette méthode, on peut montrer que "telle solution convient", pas qu'il s'agit des seules solutions possibles mais l'essentiel est ici de tester le "sens physique" des étudiants...

Posté par re : Nappe cylindrique 15-01-18 à 11:20

Bonjour
J'ai répondu hier soir à ta question sur la méthode utilisée et la justification qualitative du terme en sin(). Je viens de prendre un peu de temps pour contrôler les équations que tu as écrites. Il s'agit peut-être de simples erreurs de copie de ta part, sinon, ton corrigé contient des erreurs.
1° : concernant le vecteur champ d'induction B le long de l'axe, tu écris :

$\normalcolor \red{\vec{B(M)}=\frac{\mu_{0}M}{2}\vec{u_{z}}}$
Cette formule est certainement fausse ! Il suffit de raisonner sur les plans de symétrie et d'antisymétrie de la source de champ.
a) Tout plan perpendiculaire à (Oz) est plan d'antisymétrie de la source ; donc : en tout point M de l'espace (pas seulement le long de l'axe) le vecteur B appartient à ce plan :
En tout point M de l'espace : B_z=0.
b) Le plan (Oyz) est plan de symétrie de la source. En tout point de ce plan, le vecteur B est perpendiculaire à ce plan donc :
si x=0 alors : $\overrightarrow{B}=h(y).\overrightarrow{u_{x}}$ où h est une fonction de y à déterminer. Dans la cas particulier des points M appartenant à l'axe (Oz) :
$\overrightarrow{B}=h(0).\overrightarrow{u_{x}}$
c) remarque qui aurait dû te "mettre la puce à l'oreille" : un vecteur champ colinéaire à Oz de norme fixe pourrait être le champ créé par un solénoïde de longueur infinie et dans ce cas, la densité surfacique de courant serait de la forme :

$\vec{j_{s}}=J_{0}.\overrightarrow{u_{\theta}}\quad avec\quad J_{0}\text{ : constante}$
2° Concernant l'expression : $\normalcolor \blue{A(r,\theta )=f(r)g(\theta )}$ , l'équation :

$\frac{1}{r}\frac{\partial (rf')}{\partial r} =-\frac{g''}{g}$
est fausse car non homogène. Ecrira que le laplacien est nul en tout point conduit à :

$r\cdot\frac{d\left(r.f'\right)}{dr}=-f\cdot\frac{g''}{g}$

Remarque : sans trop anticiper sur la suite : la modélisation surfacique du courant peut introduire des discontinuités du vecteur champ B en r=R...

Posté par re : Nappe cylindrique 15-01-18 à 19:01

Bonsoir,

Je vous remercie pour vos réponses. Je m'excuse pour les fautes commises dans le corrigé. Je comprends le choix des solutions pour le potentiel vecteur maintenant. Sinon, pour montrer que le potentiel vecteur est nul pour les deux valeurs 0 et de ( bien sûr modulo 2) , est-ce que parce qu'un point de coordonnées /0 ou = , on a en plus du plan (M, $\vec{u_{r}}$ ,
$\vec{u_{\theta }}$ ) qui est dans ce cas le plan (M, $\vec{u_{x}}$ ,
$\vec{u_{y}}$ ) qui est plan d'antisymétrie, mais aussi le plan (M, $\vec{u_{x}},\vec{u_{z}}$ ) comme plan d'antisymétrie ce qui nous donne forcément le vecteur potentiel vecteur nul.
Sinon pour =/2 ou =-/2 alors comme toujours le plan (M, $\vec{u_{r}}$ ,
$\vec{u_{\theta }}$ ) est un plan d'antisymétrie, et le plan (M, $\vec{u_{y}}$ ,
$\vec{u_{z}}$ ) est un plan de symétrie, c'est pour cela qu'on a le potentiel vecteur maximal ? Je veux dire c'est comme s'il est "doublement supporté" par la symétrie ou quelque chose du genre.

Merci d'avance

Posté par re : Nappe cylindrique 15-01-18 à 19:24

OK pour ton raisonnement pour les valeurs nulles du potentiel vecteur.
Pour les extremums de A en fonction de à r fixe, j'ai simplement pris en considération la relation de définition du vecteur A :

$\overrightarrow{A_{(M)}}=\frac{\mu_{0}}{4\pi}\iint\frac{\overrightarrow{j_{s(\text{P)}}}}{\Vert\overrightarrow{PM}\Vert}\cdot dS$
À r fixe, la projection du vecteur j_s sur (Oz) possède un maximum en =/2 rad et un minimum en =-/2 rad, donc, toutes choses égales par ailleurs...

Posté par re : Nappe cylindrique 15-01-18 à 19:36

Bonsoir,

Je vois. Merci beaucoup pour votre aide. Je peux continuer maintenant avec aise .

Posté par re : Nappe cylindrique 16-01-18 à 19:48

Bonjour
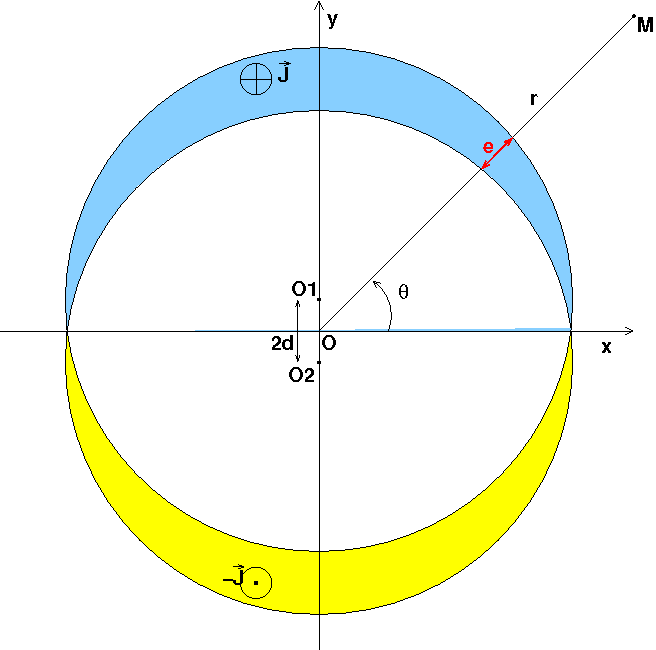
Il existe une méthode d'étude alternative à ce dispositif à mon avis plus rigoureuse mais elle suppose de bien connaître son cours sur le potentiel vecteur créé par un conducteur cylindrique. Il “suffit” de remarquer que la distribution surfacique de courant est équivalente à deux cylindres de même rayon R, l'un parcouru par un courant continu d'intensité I dans le sens montant, l'autre parcouru par un courant de même intensité dans le sens descendant, les deux axes étant parallèles à (Oz) et très légèrement décalés l'un par rapport à l'autre. L'axe du premier est en y=d, l'axe du second en y=-d avec d<<R. (pour plus de clarté : valeur de d très exagérée sur la figure). Dans la zone commune au deux cylindres, la densité du courant est nulle. Dans la zone”bleue” : $\overrightarrow{j}=\overrightarrow{J}=\frac{I}{\pi R^{2}}\overrightarrow{u_{z}}$ ; dans la zone “jaune”, la densité de courant est le vecteur opposé au précédent. L'épaisseur e étant très faible par rapport à R, chaque zone est équivalente à une densité surfacique de courant avec $\overrightarrow{j_{S}}=\overrightarrow{j}.e$ avec $e=2d.\sin\left(\theta\right)$ . On retombe bien sur la description du problème avec :
M=2J.d

Il suffit alors d'appliquer le principe de superposition, les vecteurs champ étant la somme des vecteurs champs créé par chacun des deux cylindres. Je te présente les résultats sans trop détailler :
Potentiel vecteur créé par le cylindre n° 1 seul (potentiel arbitrairement nul sur l'axe du cylindre) :
$r<R&\overrightarrow{A_{1}}=-\frac{\mu_{0}}{4}\overrightarrow{J}\cdot\Vert\overrightarrow{O_{1}M}\Vert^{2}$

$r>R&\overrightarrow{A_{1}}=-\frac{\mu_{0}}{4}\overrightarrow{J}\cdot R^{2}.\left[1+2.\ln\left(\frac{\Vert\overrightarrow{O_{1}M}\Vert}{R}\right)\right]$
Potentiel vecteur créé par le cylindre n° 2 seul :

$r<R&\overrightarrow{A_{2}}=\frac{\mu_{0}}{4}\overrightarrow{J}\cdot\Vert\overrightarrow{O_{2}M}\Vert^{2}$

$r>R&\overrightarrow{A_{2}}=\frac{\mu_{0}}{4}\overrightarrow{J}\cdot R^{2}.\left[1+2.\ln\left(\frac{\Vert\overrightarrow{O_{2}M}\Vert}{R}\right)\right]$

Théorème d'Al Khashi :

$\Vert\overrightarrow{O_{1}M}\Vert^{2}=r^{2}+d^{2}-2r.d.\sin\left(\theta\right)$

$\Vert\overrightarrow{O_{2}M}\Vert^{2}=r^{2}+d^{2}+2r.d.\sin\left(\theta\right)$

Principe de superposition :

$r<R&\overrightarrow{A}=\overrightarrow{A_{1}}+\overrightarrow{A_{2}}=\frac{\mu_{0}}{4}\overrightarrow{J}\cdot\left(\Vert\overrightarrow{O_{2}M}\Vert^{2}-\Vert\overrightarrow{O_{1}M}\Vert^{2}\right)=\mu_{0}.\overrightarrow{J}.r.d.\sin\left(\theta\right)\\r>R&\overrightarrow{A}=\frac{\mu_{0}}{2}\overrightarrow{J}\cdot R^{2}.\ln\left(\frac{\Vert\overrightarrow{O_{2}M}\Vert}{\Vert\overrightarrow{O_{1}M}\Vert}\right)$

Pour r>R , puisque d<<R, il est possible d'effectuer des développement limité au premier ordre en d/r :

$\Vert\overrightarrow{O_{1}M}\Vert=r.\left[1+\frac{d^{2}}{r^{2}}-\frac{2d}{r}.\sin\left(\theta\right)\right]^{\frac{1}{2}}\approx r\left[1-\frac{d}{r}.\sin\left(\theta\right)\right]$

$\Vert\overrightarrow{O_{2}M}\Vert=r.\left[1+\frac{d^{2}}{r^{2}}+\frac{2d}{r}.\sin\left(\theta\right)\right]^{\frac{1}{2}}\approx r\left[1+\frac{d}{r}.\sin\left(\theta\right)\right]$

$\\ \ln\left(\frac{\Vert\overrightarrow{O_{2}M}\Vert}{\Vert\overrightarrow{O_{1}M}\Vert}\right)\approx\ln\left(\frac{1+\frac{d}{r}.\sin\left(\theta\right)}{1-\frac{d}{r}.\sin\left(\theta\right)}\right)\approx\ln\left(1+2\frac{d}{r}.\sin\left(\theta\right)\right)\approx2\frac{d}{r}.\sin\left(\theta\right)$

Au final :

$r<R&\overrightarrow{A}=\mu_{0}.\overrightarrow{J}.r.d.\sin\left(\theta\right)=\mu_{0}\frac{M}{2}\cdot r\cdot\sin\left(\theta\right)\cdot\overrightarrow{u_{z}}\\r>R&\overrightarrow{A}=\mu_{0}\cdot\overrightarrow{J}.R^{2}\cdot\frac{d}{r}\cdot\sin\left(\theta\right)=\mu_{0}\frac{M}{2}\cdot\frac{R^{2}}{r}\cdot\sin\left(\theta\right)\cdot\overrightarrow{u_{z}}$

Il est toujours possible de choisir J suffisamment grand pour que d soit extrêmement petit devant R de sorte que le développement limité effectué n'introduit pas plus d'erreur que le simple fait de choisir une modélisation surfacique. D'où le passage au signe “=” .

Remarque : un autre problème, très classique aux concours (surtout aux oraux), utilise la même astuce. Il s'agit de déterminer le potentiel et le vecteur champ électrique créés en tout point par une distribution surfacique de charge sur une sphère de rayon R telle que : $\sigma=\sigma_{0}\cdot\sin\left(\theta\right)$ . On peut raisonner sur deux boules de rayon R chargées uniformément en volume avec des densités volumiques de charge et - décalées l'une par rapport à l'autre de (2d) de sorte que :

$\sigma_{0}=2\rho.d$

Nappe cylindrique