Inscription / Connexion Nouveau Sujet
Mutuelle induction de 2 solénoïdes coaxiaux
Bonjour,
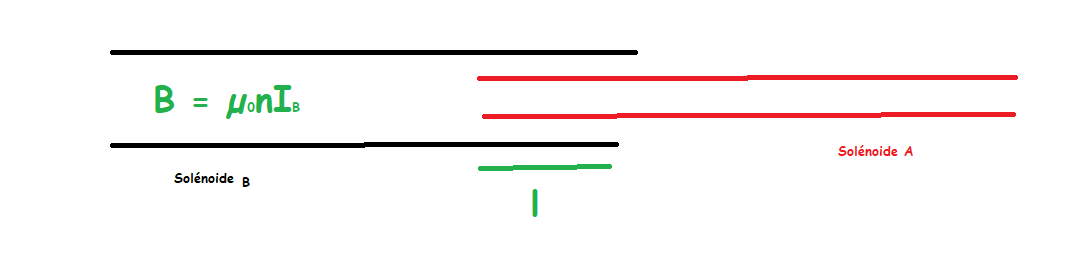
On cherche à calculer le coefficient de mutuelle induction de deux solénoïdes A et B qui se pénètrent d'une longueur l (schéma)
On nous précis qu'ils sont coaxiaux, longs et fins, parcourus par un courant I de meme sens
Pour calculer leur induction mutuelle , j'ai utilisé
D'où
Je ne suis pas sur de ma méthode, cela semble t il correct ?
Merci d'avance pour votre aide 
Bon samedi
Bonjour
L'étude rigoureuse est relativement délicate car le champ magnétique créé par le solénoïde B ( risque de confusion avec champ magnétique : pourquoi pas solénoïdes 1 et 2 ?) n'est pas nul à l'extérieur de celui-ci...
Si je comprends bien, le calcul approché consiste à considérer que le solénoïde de gauche créé au niveau du solénoïde de droite un champ magnétique uniforme sur la longueur l puis un champ nul dans le reste du solénoïde A....
Problème : tu utilises deux fois la lettre l avec deux significations physiques différentes...
Les deux solénoïde ont-ils le même nombre de spires par unité de longueur ?
Effectivement il y a confusion entre l'intensité et la longueur de "recouvrement"
On peut noter cette longueur "d"
Effectivement, j'ai considéré que la solénoïde de gauche crée un champ uniforme BG = µ0n I à l'intérieur de celui ci .
Pour calculer le flux du solénoide de Gauche sur le solénoide de droite, j'ai fais
Comme j'ai supposé BG uniforme, j'ai pu le sortir de l'intégrale et calculer la surface recouverte du solénoide de gauche, ce qui m'a donné
Aucune indication sur le nombre de spires par unité de longueur, donc je pense qu'on peut les prendre égaux ?
Merci pour votre aide 
Le solénoïde de droite contient (n.d) spires dans le champ magnétique créé par le solénoïde de droite, chaque sire étant de rayon R.
Le flux à travers le solénoïde de droite a pour expression :
BG.n.d. .R2
.R2
Je te laisse finir.


