Voilà le dessin

Bonjour,

Je vais être honnête, je ne comprends pas grand chose à ton exercice :
- qu'est-ce "Pt" (quand toi tu définis une force équivalente "Fq" non représentée sur le schéma) ?
- est-ce un système iso ou hyperstatique ?
- par quoi peut-on modéliser la liaison entre ce que j'imagine être le mure et le sol ?

Bref cet énoncé est très incomplet ...

Salut Monsieur ,
Désolé si j'ai pas bien détaillé dans mon exercice,

Premièrement ça ce n'est pas un exercice c'est une partie de cour de 'Poussée '
Je vais détaillé:  
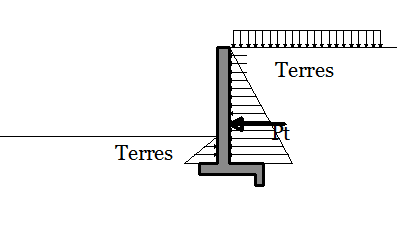
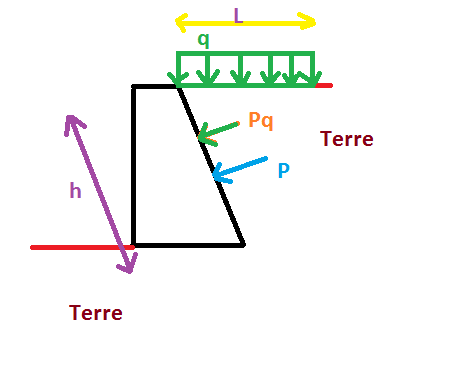
j'ai un mur de soutènement (en noir) qui soutenir la terre, donc la terre applique des petite pression qu'on a appelle une poussée P (on bleu ) la formule de cette poussée P,
P=(1/2)*Ka*G*h^2;
ka: coef de poussée de la terre,
G: poids volumique
h: la longueur (comme elle montré dans le schéma) ,

je suis bien d'accord avec cette formule (car la terre applique des petites pression, le diagramme de ces pression c'est diagramme triangulaire donc la poussée, c'est la résultante de ces ces pression donc c'est la surface de notre triangle de pression est pour ça on trouve cette formule).

Maintenant pour la surcharge q , d'après notre cour on a écrit que : quand il y a une surcharge q , cette surcharge applique aussi une poussée sur le mur Pq (en vert) et cette poussée due à la surcharge Pq=  ka.q.h ,

Mon problème:
comment on a fait la transformation de cette surcharge q à une poussée Pq , et pour quoi on a cette formule Pq=  ka.q.h ?

Merci Monsieur, et j'espère que mon problème est clair maintenant.

Salut,

Je n'ai pas étudié la méca des sols mais tes formules me font penser à celles de l'hydrostatique. A la différence près que la pression due au poids de la terre n'est pas transmise  intégralement au mur mais via un coefficient Ka qui caractérise le type de sol.
On retrouve en effet les formules d'hydrostatique

Maintenant si tu ajoutes une pression q à la surface de l'eau, elle se transmet intégralement, je veux dire par là qu'elle ne dépend pas de z. Tu dois donc simplement ajouter q à la pression :

En intégrant, tu obtiens le résultat attendu.
Pour vérifier tout ça, je te conseille de regarder la dimension (les unités) des différentes grandeurs impliquées. En particulier doivent être de même dimension. Normalement, la largeur L du mur devrait intervenir mais elle a disparu entre ton premier message et le dernier... Donc vérifie bien la cohérence de tout ça.
L'équation de moment va te donner le point d'application de la résultante des forces. On peut encore ajouter que le point d'application de la résultante Pq est situé à h/2 alors que le point d'application de P est plus bas vu que la pression augmente avec le poids de terre situé au dessus.
Des questions ?