Niveau licence

Mouvement relatif

Posté par
Rimi 30-12-16 à 14:07

Bonjour à tous, j'ai besoin d'aide pour cet exo svp et merci â l'avance
Énoncé: Un disque de rayon tourne par une vitesse angulaire =3t autour d'une axe pose par l'origine o' (o' est un point de l'axe OX')
On étudie le mouvement d'une particule M situe initialement sur la périphérie du disque , M se déplace vers le centre du disque O' par une vitesse V0=1m/s sur l'axe O'X', on considère un repère O'X'Y' fixé au centre du disque à t= 0 les axes OX et O'X' sont confondues
Montrer que le vecteur position relatif O'M=(-t+1) et déterminer la vitesse Vr de M par rapport à O'X'Y' et Ce la vitesse du repère O'X'Y' par rapport au repère OXY

Posté par re : Mouvement relatif 30-12-16 à 14:34

Bonjour
Et si tu proposais un début de solution en expliquant avec précision ce qui t'empêche de terminer ? L'aide ultérieure serait beaucoup plus efficace qu'un simple corrigé qui ne serait pas nécessairement exactement adapté à ton niveau !
Je te laisse réfléchir !

Posté par re : Mouvement relatif 30-12-16 à 18:02

Oui c'est vrai, on cherche maintenant O'M, on sait que OM=x+y j'ai essayé d'abord d'utiliser la relation de shal O'M=O'O+O'M mais on sait rien. Sur O'O , même si on ignore cette question et on passe à déterminer les vecteurs vitesses , est-ce qu'on peut écrire le vecteur = (il n'y a pas l'axe le)??

Posté par re : Mouvement relatif 30-12-16 à 18:02

Rimi @ 30-12-2016 à 18:02

Oui c'est vrai,

on cherche maintenant O'M, on sait que OM=x

j'ai essayé d'abord d'utiliser la relation de shal O'M=O'O+O'M mais on sait rien. Sur O'O , même si on ignore cette question et on passe à déterminer les vecteurs vitesses , est-ce qu'on peut écrire le vecteur

(il n'y a pas l'axe Oz)??

Posté par re : Mouvement relatif 30-12-16 à 20:57

Bonsoir
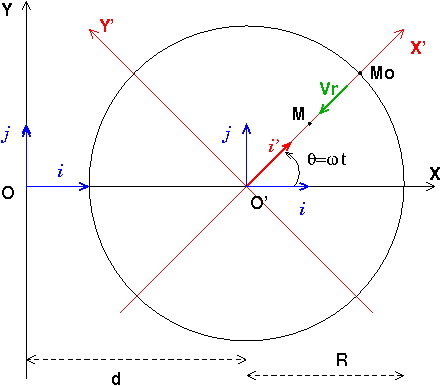
Ton énoncé est assez confus et ne comporte pas de schéma. De plus, mélanger dans une même formule lettres et chiffres est une très mauvaise idée. On ne peut pas ainsi détecter les éventuelles fautes d'homogénéité. Voici un schéma de ce que j'ai compris ; à toi d'adapter ensuite...
Je note (R) le repère absolu (O,X,Y). Je note (R') le repère relatif en rotation par rapport à (R) à la vitesse angulaire =3rad/s autour d'un axe passant par O' perpendiculaire au plan de figure. Je suppose la distance OO' fixe et égale à d.
Étude du mouvement relatif (mouvement par rapport à (R') :
C'est un mouvement rectiligne uniforme le long de l'axe (OX') à la vitesse relative :

$\overrightarrow{V_{r}}=-V_{0^,}\overrightarrow{i^{,}}$
Cette vitesse étant fixe la distance parcourue le long de l'axe entre l'instant initial et la date t quelconque est : MoM=Vo.t ; O'M=R-Vo.t ;

$\overrightarrow{O^,M}=\left(R-V_{O}\cdot t\right)\overrightarrow{i^{,}}$

Mouvement dans le repère absolu (R) :
Plusieurs méthodes sont possibles. Une simple consiste à exprimer le vecteur unitaire i' en fonction des vecteurs i et j :

$\overrightarrow{i^{,}}=\overrightarrow{i}\cdot\cos\left(\theta\right)+\overrightarrow{j}\cdot\sin\left(\theta\right)\quad avec\quad\theta=\omega\cdot t$
Ensuite, comme tu l'as déjà écrit :

$\overrightarrow{OM}=\overrightarrow{OO^{,}}+\overrightarrow{O^{,}M}=\left[d+\left(R-V_{0}\cdot t\right)\cdot\cos\left(\omega.t\right)\right]\overrightarrow{i}+\left(R-V_{0}\cdot t \right)\cdot\sin\left(\omega.t\right)\cdot\overrightarrow{j}$
Les coordonnées du point M à la date t dans (R) sont ainsi :

$\begin{cases} \\ x=d+\left(R-V_{0}\cdot t\right)\cdot\cos\left(\omega.t\right)\\ \\ y=\left(R-V_{0}\cdot t\right)\cdot\sin\left(\omega.t\right) \\ \end{cases}$
Les coordonnées du vecteur vitesse de M dans (R) sont les dérivées par rapport au temps des coordonnées précédentes :

$\begin{cases} \\ V_{x}=-V_{0}\cdot\cos\left(\omega.t\right)-\omega.\left(R-V_{0}.t\right).\sin\left(\omega.t\right)\\ \\ V_{y}=-V_{0}\cdot\sin\left(\omega.t\right)+\omega.\left(R-V_{0}.t\right).\cos\left(\omega.t\right) \\ \end{cases}$
Si tu as vu le cours correspondant, je te laisse retrouver ce résultat en utilisant la relation de composition des vitesses.
Je me répète : tout cela est sous réserve : n'ayant pas le schéma ni les question précises... Je pense tout de même que cela va t'aider !

Mouvement relatif