Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Mouvement plan sur plan

Posté par
Ariel60 30-11-17 à 12:29

Bonjour,
Je m'excuse encore pour les questions;j'aurai vraiment besoin de votre aide avec cet exercice...:
Dans le plan (Πo)=(Oo,\vec{x_0},\vec{y_0},\vec{z_0}),on considère les points A(R,0)et B(-R,0) où R réel positif donné(cte).Le plan (Π)=(O,\vec{x},\vec{y},\vec{z}) est mobile sur le plan Πo de façon que l'axe (O,x) passe constamment par B et l'axe (O,y) par A et que  (\vec{x_0},\vec{u})=wt avec wt =cte >0 et \vec{u}=\vec{OoO}
1)Déterminer le centre instantané de rotation ,la base et la roulante du mouvement de Π sur Πo
2)Déterminer le point lié à Π dont l'accéleration est nulle à l'instant t.On appelle ce point le centre d'accéleration J.Quelle est lorsque t varie l'ensemble des positions de J et dans Π
Merci inifiment

Posté par
vanoisere : Mouvement plan sur plan 30-11-17 à 15:26

Bonjour
Si j'ai bien compris l'énoncé, le schéma décrivant la situation devrait ressembler à celui-ci-dessous et devrait pouvoir t'aider. Ce n'est sans doute pas un hasard si l'énoncé note R la distance de Oo à A et la distance de Oo à B.
Le triangle (AOB) est rectangle en O et tu connais sûrement la relation entre angle au centre et angle inscrit...

Mouvement plan sur plan

Posté par
diracre : Mouvement plan sur plan 30-11-17 à 16:19

Hello

Message pour vanoise qu'Ariel60 ne doit surtout pas lire

1) tout d'abord bonjour à toi 2) avec geogebra ci dessous le schéma que j'obtiens et je ne crois pas que cela tienne au logiciel ... où commets je (?) une erreur?

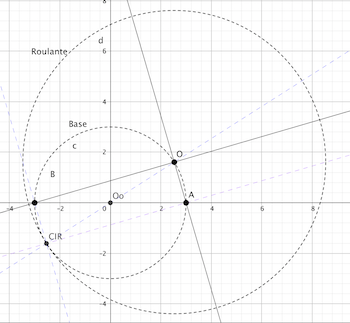
Mouvement plan sur plan

Posté par
vanoisere : Mouvement plan sur plan 30-11-17 à 16:48

Bonjour Dirac
Le but de mon schéma est juste de suggérer que le point O se déplace sur un cercle de centre Oo  et de rayon R  puis que le vecteur rotation instantanée de (R) par rapport à Ro est

\overrightarrow{\Omega}=\frac{\omega}{2}\overrightarrow{U_{zo}}
information qui, à la réflexion, n'est pas indispensable à la résolution du problème.
Je me suis bien gardé d'indiquer le centre instantané de rotation, la base et la roulante !
A la réflexion, tracer le second cercle comme je l'ai fait peut plus induire en erreur qu'aider : tu viens d'en fournir la preuve !
Maintenant, avec ton schéma : si Ariel60 ne s'en sort pas !

Posté par
diracre : Mouvement plan sur plan 30-11-17 à 16:58

  Ariel60 ayant scrupuleusement suivi la consigne de mon précédent msg tt va bien . Je n'avais pas "percuté" sur le = /2: cela propose un raisonnement où les conclusions tombent au moins aussi. Je vais le mémoriser.

Posté par
vanoisere : Mouvement plan sur plan 30-11-17 à 17:23

Rebonsoir dirac,
puisque tu sembles présent sur ce forum ce soir, j'aurais une question à poser à propos du problème sur le pendule simple que tu viens de corriger (ccp2013).
Tu as été bien courageux : bravo ! J'espère que VINCENZ0O va apprécier à sa juste valeur !
Il s'agit de la question consistant à démontrer que, la pseudo force de Coriolis pouvant être négligée, le mouvement du pendule est plan quand celui-ci est écarté de sa position d'équilibre et abandonné sans vitesse initiale. Comme membre de jury, je l'ai rencontré deux fois. Je n'ai jamais trouvé un étudiant capable de s'en sortir. Beaucoup "sautent" la question (attitude judicieuse vue la longueur de l'épreuve), les autres évoquent la conservation du moment cinétique par analogie avec l'étude des forces centrales, ce qui évidemment est faux ! Beaucoup d'ouvrages considère la réponse comme intuitivement évidente et élude le problème. La seule démonstration que je connaisse est un peu lourde. Elle consiste à découper le mouvement par tranches successives de durée t très courte par rapport à la période. Je te la fais brève :
- soit le plan vertical contenant le pendule à la date t=0 ; la vitesse intiale étant nulle et l'accélération initiale étant un vecteur appartenant à , le pendule est dans le plan à t=t. A cette date, les vecteur vitesse et accélération appartenant à , le pendule à la date 2t sera dans le plan et aura un vecteur vitesse et un vecteur accélération appartenant à   et ainsi de suite...
Je t'avais prévenu... Si tu connais mieux, je suis bien sûr preneur !

Posté par
diracre : Mouvement plan sur plan 30-11-17 à 19:01

reHello vanoise (Ariel60, promis, après on te rend ton sujet )

J'avais bien conscience de "bâcler" la réponse à la première question, mais il y en avait une quarantaine derrière. Je crois qu'en "conditions réelles" je l'aurais peaufinée un peu plus. J'y réfléchis et je te soumettrai pour critique la rédaction "optimale selon dirac" de cette 1ere réponse  
De toute façon il y a encore une 10 zaine de question dans le sujet qu'il faut que je traite. Un sujet pas vraiment passionnant (peut être à la fin?) mais qui doit bien occuper les 4 heures d'examen.

Posté par
Ariel60re : Mouvement plan sur plan 01-12-17 à 12:38

Bonjour,
Merci encore pour votre contribution,
Pour la 1),j'ai trouvé comme CIR:
\vec{OI}=\frac{-2}{w}[Rwsinwt \vec{y_0}+Rwcos wt\vec{x_0}];
Pour la base j'ai trouvé comme équations paramétriques:x_0=2Rcos wt; y_0=-2Rsin wt
Pour la roulante:x(t)=-2Rcos wt.(\frac{1}{cos(wt/2)}); y(t)=-2Rsin wt.(\frac{1}{cos(wt/2)})
Corrigez-moi je vous en supplie
Merci infiniment

Posté par
diracre : Mouvement plan sur plan 01-12-17 à 18:45

Hello

Concernant I, cela serait chouette que:
- tu simplifies l'expression \\ - notes que \vec{OOo} = -\vec{OI}
- tire explicitement les conclusions de cette expression vectorielle

Concernant la base:
Le résultat que tu obtiens est incorrect. Peux tu détailler les étapes de ton raisonnement afin de pouvoir t'aider? (Mon conseil étant de t'aider des résultats obtenus en ce qui concerne le CIR)


Concernant la roulante:
Idem. Détaille ton raisonnement afin que nous puissions t'aider à identifier l'endroit où ça coince.

Posté par
Ariel60re : Mouvement plan sur plan 01-12-17 à 19:44

Bonjour,
Base:trajectoire de I dans Πo,donc j'utilise l'expression de OI dans Πo.
Roulante:trajectoire de I dans Π,j'exprime OI dans Π et je sors x(t) et y(t).
Cordialement

Posté par
diracre : Mouvement plan sur plan 01-12-17 à 20:18

hum hum ...

Tu établis:

\vec{OI}=\frac{-2}{w}[Rwsinwt \vec{y_0}+Rwcos wt\vec{x_0}]

Donc \vec{OI}=-2Rcos wt\vec{x_0}-2Rsinwt \vec{y_0} = -2\vec{OoO}

Soit  \vec{OI} = 2\vec{OOo}

Oo est le milieu de [OI], Or O décrit un cercle de rayon R aide centre Oo dans le repère {Oo,x0,yo}

La base est donc le cercle de centre Oo et de rayon R

Par ailleurs:

\vec{OI}=-2Rcos wt\vec{x_0}-2Rsinwt \vec{y_0} = -2\vec{OoO}

Donc à tout instant:  OI = 2R

La roulante est le cercle de rayon 2R est de centre O

On a bon?

(La mécanique en générale celle des solides en particulier est présentée avec des formalismes différents selon les cursus, donc je ne suis pas certain que ce raisonnement qui me semble le plus efficace, corresponde à la façon dont ton cours est organisé, tu n'hésites pas à "sonner" si besoin)

Posté par
Ariel60re : Mouvement plan sur plan 04-12-17 à 16:04

Bonjour,
Je ne comprends pas comment vous avez déterminé la base alors que dans (Πo)=(x_0,y_0,z_0) on a OI=2OOodonc x^2+y^2=4R^2 (cercle de centre Oo et de rayon 2R).Et puis dans 2),j'ai trouvé \vec{V_{\pi 0} }(J\in\pi)=(w/2)\vec{z_0}\Lambda (x \vec{x_0}+y \vec{y_0})=\vec{cte} mais là comment déterminer x et y?
J'excuse encore pour les questions qui peuvent paraître assez bêtes mais on n'a jamais fait cet exercice en TD alors..

Posté par
diracre : Mouvement plan sur plan 04-12-17 à 18:36

La base est la trajectoire du CIR (point I) dans le repère (Oo, xo, yo)

Donc tu vas chercher à exprimer le vecteur \vec{O_0I} en fonction de \vec{x_0} et \vec{y_0}

Tu avais établis:

\vec{OI}=-2Rcos wt\vec{x_0}-2Rsinwt \vec{y_0}

Donc

\vec{O_0I}=\vec{O_0O} -2Rcos wt\vec{x_0}-2Rsinwt \vec{y_0}

Or

\vec{O_0O}= Rcos wt\vec{x_0} + Rsinwt \vec{y_0}

Donc

\vec{O_0I}= -Rcos wt\vec{x_0}-Rsinwt \vec{y_0}

La trajectoire est bien le cercle de centre Oo et de rayon R: le CIR est à chaque instant le point de ce cercle diamétralement opposé à O.

Posté par
vanoisere : Mouvement plan sur plan 05-12-17 à 11:22

Bonjour dirac, bonjour Ariel 60
Histoire d'utiliser ma remarque du   30-11-17 à 16:48 sur le vecteur rotation instantané, voici une méthode alternative rapide mais peut-être pas au programme d'Ariel60. Elle suppose connue la relation de "champ de vitesse d'un solide", c'est à dire la relation permettant d'obtenir la vitesse d'un point quelconque d'un solide en fonction de la vitesse d'un point particulier de celui-ci et du vecteur rotation instantané. Pour un point M quelconque fixe dans R :

\overrightarrow{V_{(M/R_{0})}}=\overrightarrow{V_{(O/R_{0)}}}+\overrightarrow{\Omega_{(R/R_{0})}}\wedge\overrightarrow{OM}

Appliqué au cas particulier du point I de vitesse nulle dans Ro :

\overrightarrow{V_{(I/R_{0})}}=\omega\cdot\overrightarrow{u_{z}}\wedge\overrightarrow{O_{0}O}+\frac{\omega}{2}\cdot\overrightarrow{u_{z}}\wedge\overrightarrow{OI}=\frac{\omega}{2}\cdot\overrightarrow{u_{z}}\wedge\left(\overrightarrow{OI}+2\overrightarrow{O_{0}O}\right)=\overrightarrow{0}

Les vecteurs OI et OoO étant nécessairement orthogonaux à Uz, la condition précédente conduit simplement à :

\overrightarrow{OI}=-2\overrightarrow{O_{0}O}

Résultat déjà obtenu par les autres méthodes.

Posté par
diracre : Mouvement plan sur plan 05-12-17 à 12:05

Re-hello

Tes expressions en 2/omega et 1/cosinus ainsi que le OI en omega t (plutôt qu'en 1/2omega t) me turlupinent car je ne "vois" pas à quelle étape du raisonnement/calcul tu peux les faire apparaître ... Je crois donc utile de récapituler pour éviter les malentendus:

Pour  M \in (\Pi)
\vec{O_0M} = x_0.\vec{x}_0 + y_0.\vec{y}_0=\vec{O_0O}+\vec{OM}
\vec{OM} = x.\vec{x} + y.\vec{y}

Avec, du fait du mouvement de (\Pi)  dans (\Pi_0)

\vec{O_0O} = cos\omega t.\vec{x}_0+sin\omega t.\vec{y}_0

\vec{x} = cos\frac{\omega}{2}t.\vec{x}_0+sin\frac{\omega}{2}t.\vec{y}_0
\vec{y} = -sin\frac{\omega}{2}t.\vec{x}_0+cos\frac{\omega}{2}t.\vec{y}_0

Avec au passage:

\vec{x}_0 = cos\frac{\omega}{2}t.\vec{x}-sin\frac{\omega}{2}t.\vec{y}
\vec{y}_0 = sin\frac{\omega}{2}t.\vec{x}+cos\frac{\omega}{2}t.\vec{y}

Donc:

\vec{O_0M} = (Rcos\omega t +xcos\frac{\omega}{2}t-ysin\frac{\omega}{2}t).\vec{x}_0+(Rsin\omega t +xsin\frac{\omega}{2}t+ycos\frac{\omega}{2}t).\vec{y}_0        (Eq. 1)

Et la vitesse de M est:

\frac{d}{dt}\vec{O_0M} = -\omega(Rsin\omega t +\frac{x}{2}sin\frac{\omega}{2}t+\frac{y}{2}cos\frac{\omega}{2}t).\vec{x}_0+\omega(Rcos\omega t +\frac{x}{2}cos\frac{\omega}{2}t-\frac{y}{2}sin\frac{\omega}{2}t).\vec{y}_0.   (Eq.2)

I étant le point tel que  \frac{d}{dt}\vec{O_0I} =\vec{0}

On a en I

Rsin\omega t +\frac{x}{2}sin\frac{\omega}{2}t+\frac{y}{2}cos\frac{\omega}{2}t = 0
Rcos\omega t +\frac{x}{2}cos\frac{\omega}{2}t-\frac{y}{2}sin\frac{\omega}{2}t = 0

Soit:

xsin\frac{\omega}{2}t+ycos\frac{\omega}{2}t =-2Rsin\omega t
xcos\frac{\omega}{2}t-ysin\frac{\omega}{2}t =-2Rcos\omega t

Et donc en réinjectant ces expressions dans Eq. 1:

\vec{O_0I} = (Rcos\omega t-2Rcos\omega t).\vec{x}_0+(Rsin\omega t-2Rsin\omega t).\vec{y}_0        

On trouve bien le résultat attendu:

\vec{O_0I} = -Rcos\omega t.\vec{x}_0-Rsin\omega t.\vec{y}_0 = - \vec{O_0O}      

Pour la roulante:

\vec{OI} = 2\vec{O_0I}

Donc:

\vec{OI} = -2R(cos\omega t(cos\frac{\omega}{2}t.\vec{x}-sin\frac{\omega}{2}t.\vec{y}) + sin\omega t(sin\frac{\omega}{2}t.\vec{x}+cos\frac{\omega}{2}t.\vec{y}))

Soit:

\vec{OI} = -2R(cos\frac{\omega}{2}t.\vec{x}+sin\frac{\omega}{2}t.\vec{y}))

Pour le point J où l'accélération est nulle, il te suffit de prendre l'équation Eq. 2 et de la dériver une nouvelle fois par rapport au temps.

On a bon? (sauf étourderie/copier-coller Latex malheureux)

Posté par
diracre : Mouvement plan sur plan 05-12-17 à 12:09

Hello vanoise,

Désolé, je n'ai pas cliqué sur "vérifier" tellement occupé à "vérifier" ma syntaxe!

Comme cela Ariel aura une méthode élégante et une méthode besogneuse ...

Posté par
Ariel60re : Mouvement plan sur plan 07-12-17 à 20:52

Bonsoir,
Encore merci pour votre aide!J'ai trouvé pour J \vec{OoJ}=[\frac{3}{4}sin( wt/2 )+\frac{3}{4}x cos(wt/2) ]\vec{x_o}+[\frac{3}{4}x sin(wt/2)+\frac{3}{4}y cos(wt/2)]\vec{y_o}
Est-ce bien cela?
Cordialement

Posté par
diracre : Mouvement plan sur plan 08-12-17 à 09:03

hum hum ...

Il y a une petite coquille dans le 1er terme qui est \frac{3}{4}sin...

Plus "grave" ... en écrivant \vec{O_0J} sous cette forme, tu n'avances pas bcp dans la détermination de la courbe parcourue par J dans (\Pi_0) puisque tu mixe le repère (\vec{x}_0,\vec{y}_0) de ce plan et les coordonnées dans l'autre plan.

Et pourtant tu y étais presque

Tu as pour sûr calculé:

\frac{d^2}{dt^2}\vec{O_0M} = -\omega^2(Rcos\omega t +\frac{x}{4}cos\frac{\omega}{2}t-\frac{y}{4}sin\frac{\omega}{2}t).\vec{x}_0+\omega^2(-Rsin\omega t -\frac{x}{4}sin\frac{\omega}{2}t-\frac{y}{4}cos\frac{\omega}{2}t).\vec{y}_0.   (Eq.3)

Et donc: frac{d^2}{dt^2}\vec{O_0J} = \vec{0}

Conduisant à:

xsin\frac{\omega}{2}t+ycos\frac{\omega}{2}t =-4Rsin\omega t  
xcos\frac{\omega}{2}t-ysin\frac{\omega}{2}t =-4Rcos\omega t  

Mais ce sont le premiers termes qu'il faut substituer dans Eq 3 pour obtenir:

\vec{O_0J} = -3Rcos\omega t.\vec{x}_0-3Rsin\omega t.\vec{y}_0     

La courbe est donc un cercle de centre O0et de rayon 3R



A toi pour la courbe dans (\Pi)? Et aussi pour retrouver J également par la méthode proposée par vanoise?

Posté par
Ariel60re : Mouvement plan sur plan 14-12-17 à 21:02

Bonsoir,
Encore merci pour les explications,
Pour la courbe dans (Π),j'exprime \vec{OJ}=\vec{OOo}+\vec{OoJ}
dans (Π) alors je trouve \vec{OJ}=(-4Rcos^2wt-4Rsinwt .sin(wt/2))\vec{x}+(-4Rcoswt .sin wt -4Rsinwt .cos(wt/2))\vec{y}
avec \vec{x_o}=coswt \vec{x}+sin wt \vec{y};\vec{y_o}=sin(wt /2)\vec{x}+cos (wt/2) \vec{y}
Je ne comprends pas pourquoi ça ne donne toujours pas de courbe remarquable..
Cordialement

Posté par
vanoisere : Mouvement plan sur plan 15-12-17 à 11:49

Bonjour
Je laisse dirac répondre à tes questions sur le travail que tu viens d'exposer. Je me permets tout de même de donner suite à mon message du   05-12-17 à 11:22 qui permet assez rapidement d'obtenir le résultat sur I et sur J. Je continue d'appeler Ro un repère lié à o et R un repère lié à . La formule du "champ de vitesse" que j'ai déjà utilisée, appliquée au point J conduit à :

\overrightarrow{V_{(J/R_{0})}}=\omega\cdot\overrightarrow{u_{z}}\wedge\overrightarrow{O_{0}O}+\frac{\omega}{2}\cdot\overrightarrow{u_{z}}\wedge\overrightarrow{OJ}=\frac{\omega}{2}\cdot\overrightarrow{u_{z}}\wedge\left(\overrightarrow{OJ}+2\overrightarrow{O_{0}O}\right)=\frac{\omega}{2}\cdot\overrightarrow{u_{z}}\wedge\left(\overrightarrow{O_{0}J}+\overrightarrow{O_{0}O}\right)

Sachant que le vecteur \frac{\omega}{2}\cdot\overrightarrow{u_{z}}  est un vecteur fixe de Ro en aucun cas colinéaire au vecteur \left(\overrightarrow{O_{0}J}+\overrightarrow{O_{0}O}\right), une accélération nulle de J se traduit par :

\frac{d\overrightarrow{V_{(J/R_{0})}}}{dt}=\overrightarrow{0}\quad soit\quad\frac{d\left(\overrightarrow{O_{0}J}+\overrightarrow{O_{0}O}\right)}{dt}=\overrightarrow{0}\quad soit\quad\overrightarrow{V_{(J/R_{0})}}+\overrightarrow{V_{(O/R_{0})}}=\overrightarrow{0}

Soit en utilisant les expressions précédentes :

\frac{\omega}{2}\cdot\overrightarrow{u_{z}}\wedge\left(\overrightarrow{O_{0}J}+\overrightarrow{O_{0}O}\right)+\omega\cdot\overrightarrow{u_{z}}\wedge\overrightarrow{O_{0}O}=\frac{\omega}{2}\cdot\overrightarrow{u_{z}}\wedge\left(\overrightarrow{O_{0}J}+3\overrightarrow{O_{0}O}\right)=\overrightarrow{0}


Puisque \left(\overrightarrow{O_{0}J}+3\overrightarrow{O_{0}O}\right) ne peut être colinéaire à \frac{\omega}{2}\cdot\overrightarrow{u_{z}} , la condition précédente est équivalente à :

\boxed{\overrightarrow{O_{0}J}=-3\overrightarrow{O_{0}O}}

Facile alors d'obtenir le lieu des points J.

Posté par
diracre : Mouvement plan sur plan 15-12-17 à 19:25

Pour continuer avec la méthode la moins élégante donc:

\vec{OJ}=\vec{OOo}+\vec{OoJ}

Avec:

\vec{OO_0} = -Rcos\omega t.\vec{x}_0-Rsin\omega t.\vec{y}_0    


\vec{O_0J} = -3Rcos\omega t.\vec{x}_0-3Rsin\omega t.\vec{y}_0    

Donc

\vec{OJ} = -4Rcos\omega t.\vec{x}_0-4Rsin\omega t.\vec{y}_0    

Et avec:

\vec{x}_0 = cos\frac{\omega}{2}t.\vec{x}-sin\frac{\omega}{2}t.\vec{y}
\vec{y}_0 = sin\frac{\omega}{2}t.\vec{x}+cos\frac{\omega}{2}t.\vec{y}

Donc \vec{OJ} = -4R(cos\omega t.\vec{x}_0+sin\omega t.\vec{y}_0)    

Soit

\vec{OJ} = -4R[(cos\omega t.cos\frac{\omega}{2} +sin\omega t.sin\frac{\omega}{2}t )\vec{x}+(sin\omega t.cos\frac{\omega}{2}t-cos\omega t.sin\frac{\omega}{2}t)\vec{y}]    

Soit

\vec{OJ} = -4R(cos\frac{\omega}{2} t.\vec{x}+sin\frac{\omega}{2}t.\vec{y})    

J parcourt une cercle de rayon 4R et de centre O

Ariel 60, on a bon cette fois? Sois plus "structuré" dans ta méthode de résolution: on établit "facilement" dans un 1er temps OJ dans las bas x0, y0, puis on effectue le chgt de base


(Grand merci au passage à vanoise pour avoir fait avancer la résolution du problème selon une   méthode plus "vectorielle")

Posté par
Ariel60re : Mouvement plan sur plan 23-12-17 à 13:16

Je vous remercie encore pour toutes les explications,maintenant je me rend bien compte de mon erreur sur les calculs ..


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !