Inscription / Connexion Nouveau Sujet
Mouvement oscillatoire sur un plan incliné
enzoooooo
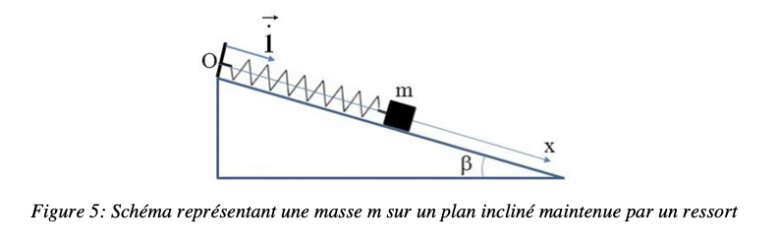
Soit un objet, assimilé à un point matériel, de masse m, et assujetti à se déplacer sur un plan incliné faisant un angle β avec l'horizontale. L'objet est attaché à un ressort à spires non jointives, de raideur k et de longueur à vide ℓ. L'axe Ox est orienté vers le bas et a pour origine O, l'extrémité fixe du ressort (voir figure 1).
Figure 5: Schéma représentant une masse m sur un plan incliné maintenue par un ressort
On se place tout d'abord dans le cas où les forces de frottement sont négligées.
1) Faire un schéma sur lequel vous ferez apparaître les forces s'exerçant sur l'objet lorsque le ressort est en extension, c'est-à-dire lorsque ℓ(t), la longueur du ressort à un instant t, est supérieure à ℓ0
.
2) Déterminer la position d'équilibre ℓe en fonction de m, g, k, β et ℓ0 .
3) Etude du mouvement sans frottement
a. Etablir l'équation différentielle du mouvement. On posera x(t) = ℓ(t) − ℓe pour obtenir une équation différentielle homogène.
b. A t=0, on écarte l'objet de 5 cm par rapport à sa position d'équilibre et on le lâche sans vitesse initiale. Déterminer l'expression de x(t). Déterminer la pulsation propre ω0 et la période propre T0 en fonction de k et m.
4) Etude du mouvement avec frottement fluide
Le montage est maintenant entièrement plongé dans un fluide visqueux, et l'objet est désormais soumis à une force de frottement proportionnelle et opposée à la vitesse telle que: f(vecteur) = −αv.
a. Etablir la nouvelle équation différentielle du mouvement en ℓ(t) puis en x(t). Montrer que cette nouvelle équation se met sous la forme canonique : ¨x(t) + 2lambda x'(t) + ω0²x(t) = 0. Donner l'expression de λ en fonction de α et m.
b. On souhaite que l'objet s'arrête à sa position d'équilibre le plus rapidement possible. Dans ces conditions, donner l'expression du coefficient de frottement α = αc en fonction de k et de m. Comment appelle-t-on ce type de mouvement ?
c. Dans le cas où α = αc, déterminer l'expression de x(t) sachant qu'à t=0s, on écarte l'objet de 5 cm par rapport à sa position d'équilibre et on le lâche sans vitesse initiale.
d. Que se passe-t-il si α < αc et si α > αc ? Décrire le mouvement et préciser le nom du régime ainsi que la forme générale de x(t) dans chaque cas.
J'ai certains doute sur mes réponses aux question 2) et 3a) que j'ai fait mais savoir si ce que j'ai fais est correct s'il vous plait ?
Pour la 2) :
P + Fr + N = 0 (Fr --> Force de rappel)
<--> mg-k(le-lo) = 0
<--> (mg)/k = le-lo
<--> le = (mg/k)+lo
Pour la 3)a : (je poste en piece jointe car je suis pas très douet avec l'informatique)
Voici ma réponse 3)a en pièce jointe
Merci d'avance pour votre aide
** image supprimée **
* modération> Image effacée. Merci d'utiliser les outils mis à ta disposition pour écrire les formules mathématiques 
*
[***A LIRE AVANT D'AGIR***] Règles du forum
ne saurais-tu pas lire ? Bonjour
La projection du poids sur l'axe des x fait intervenir l'angle d'inclinaison. Sinon : le règlement du forum demande de ne pas scanner les solutions sous forme d'image mais de les copier
vanoisevanoisevanoise
Bonjour
La projection du poids sur l'axe des x fait intervenir l'angle d'inclinaison. Sinon : le règlement du forum demande de ne pas scanner les solutions sous forme d'image mais de les copier
Comment peut on faire intervenir B (béta) dans la formule du poids .?
La projection du poids sur l'axe des x est :
Px=m.g.sin(
)
Sans avoir compris la méthode de projection des vecteurs dans une base, tu risques d'être systématiquement bloqué en physique, surtout en mécanique ! Voir ce document par exemple :
Bonjour,
je reprends ce sujet car j'ai exactement le même exercice.
Je suis bloqué à la question 4 a)…
Je ne comprends pas comment établir la nouvelle équation différentielle en l(t) . J'ai pensé par passer par la situation d'équilibre mais cela ne fonctionne pas.
Pouvez-vous m'aider s'il vous plaît ?
Bonjour
Question 3a plutôt que 4a ? Je ne trouve pas de question 4a...
La fore exercée par le ressort sur le solide de masse m peut s'écrire :
soit :
où a été obtenu lors de l'étude de la position d'équilibre. Cette condition d'équilibre conduit à une simplification importante du résultat.
Bonsoir vanoise,
Non non je suis bien bloqué a la 4a.
Pour la partie sans frottement, que j'ai déjà faite j'ai trouver l'équation différentielle suivante : avec
donc la solution est de la forme :
On résout grâce aux conditions initiales, on trouve et
Donc
la pulsation propre est égale à
et la période propre est égale à
OK.
Pour 4a : tu reprends l'étude faite sans frottement et tu ajoute la force de frottement appliquée au solide de masse m :
Après avoir divisé tous les termes par m, tu vas faire apparaître deux constantes :
et
Ce changement de variable allège les notations pour la résolution de l'équation différentielle.
Pour la résolution de l'équation différentielle du second ordre obtenue, tu dois revoir ton cours. Tu peux éventuellement t'aider aussi du document suivant en posant K=0 :
D'accord pour cela mais c'est l'équation pour x(t), ce que je ne comprends c'est pourquoi on nous demande "d'Etablir la nouvelle équation différentielle du mouvement en ℓ(t)" puis en x(t) .
Pour l'équation en x(t) je savais mais on a jamais parler dans mon cours d'une équation différentielle en l(t)...
Pouvez vous m'expliquer s'il vous plaît?
Inutile de te tracasser pour cela. Il s'agit juste d'une question de notation. Puisque : x=(l(t)-le) avec le : constante, l'accélération peut s'écrire indifféremment :
d'accord, je comprends mieux. Je vous remercie car je ne comprenais pas cette histoire de l(t). Si j'ai d'autre problème je reviendrais vers vous. Merci encore
Bonjour, je reprend le sujet.
Je suis bloqué à la question 3b., Je ne sais pas s'il faut calculer ω0 avec les donner du problème ou juste donner son expression donné par le cours.
Merci d'avance
Bonjour Traketeur,
Sache que moi j'ai juste défini en fonction de k et de m comme le demande la consigne, de plus tu ne peux le calculer tu n'as aucune valeur de k ni de m.
Oui je vois mais je pensait qu'avec x0=5cm il y avait un moyen de trouver ω0 en arrangeant l'équation. Mais bon je vais faire plus simple et montrer la l'expression de ω0 comme tu l'a fait
Merci de ta réponse
Annuler
connectez vous