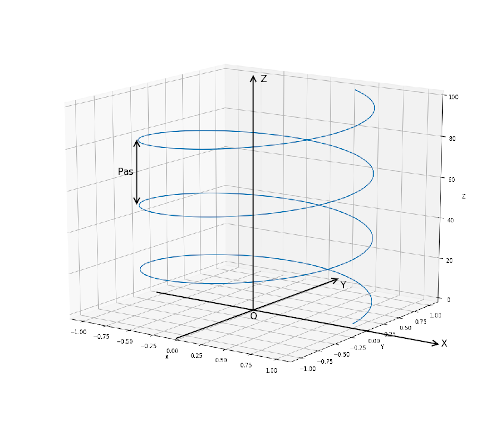
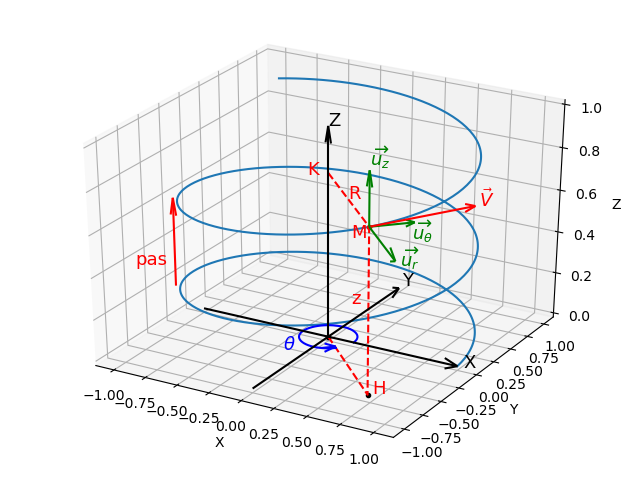
Un point M décrit une hélice, d'axe Oz vertical. L'équation de sa trajectoire en coordonnées cylindriques est donnée par : ρ(t)=R, θ(t)=ωt,z(t)=αt    
R, ω et α étant des constantes positives.

1 .Exprimer le pas p de l'hélice (en fonction de α et ω) défini comme la variation de la cote z quand le point fait un tour.

2 .Exprimer les vecteurs vitesse v et accélération a du point M dans la base cylindrique en fonction de R, α et ω. Représenter ces vecteurs sur un schéma.

3 .Définir le mouvement de M comme combinaison de 2 mouvements.

4 .Exprimer les modules des vecteurs vitesse et accélération. 5 .Montrer que la tangente à la trajectoire fait un angle constant avec l'axe Oz.

Exprimer le cosinus de cet angle Ψ en fonction de R, α et ω.


6 .Exprimer le rayon de courbure en fonction de R, α et ω.

7 .Calculer la distance lt parcourue pendant le temps t en fonction de t,R,α et ω. A.N. : t=9s,H=10m,R=2m et p=2 m où H est la hauteur parcourue pendant l'intervalle [0,t]. Pour les valeurs ci-dessus, donner lt et les autres constantes du problème.

1. Je bloque dès la première question. Je ne comprends pas bien ce qu'est le pas p de l'hélice..