Inscription / Connexion Nouveau Sujet
Mouvement et énergie potentielle
Salut, je suis bloqué sur l'exercice suivant:
Soit une particule de masse soumise à une énergie potentielle de la forme
. Déterminer le portrait de phase et la période du mouvement.
Évidemment j'ai appliqué le théorème de l'énergie mécanique, ce qui m'a donné , mais je vois pas comment aller plus loin.
Y a-t-il des méthodes pour ce genre d'exercice avec un potentiel continu mais non dérivable? Ce potentiel (qui ne peut visiblement pas découler d'une force en particulier) est-il réalisable physiquement?
Bonjour
Pour étudier le réalisme de ce problème,tu pourrais commencer par te demander à quelle force peut correspondre une telle énergie potentielle .
Justement, si ce potentiel était associé à une force elle serait de la forme , donc elle ne serait pas définie en 0 et vaudrait
sinon, et je ne connais pas de force de cette forme.
Il s'agit tout simplement d'une force d'intensité constante dont le sens s'inverse au passage en x=0.
Tu as ici une cuvette de potentiel et donc possibilité d'oscillations qui bien sûr ne sont pas sinusoïdale puisque le puits de potentiel n'est pas parabolique.
D'accord, mais comment le montrer? Habituellement on dérive l'équation obtenue à partir des théorèmes énergétiques pour obtenir l'équation du mouvement, ici cela semble hors de propos.
La particule est soumise à une force de rappel qui tend en permanence à ramener la particule en x=0 comme pourrait le faire un ressort mais avec tout de même une différence : ici, la force est de norme constante.
L'équation différentielle doit être résolue "par morceaux" suivant le signe de x mais les solutions sont particulièrement simples, du niveau terminale :
La courbe représentant les variations de x en fonction de t n'est pas une sinusoïde mais une succession de branches de parabole donnant sensiblement la même allure...
Alors je pense avoir trouvé la période des oscillations observées: En notant , on a que
. J'ai du mal pour le portrait de phase cependant...
Je n'obtiens pas tout à fait ton expression de la période. Peux-tu préciser ton calcul ?
PS : il peut être intéressant de commencer par exprimer l'amplitude du mouvement xm en fonction des conditions initiales car ensuite, la période s'exprime très simplement en fonction de cette amplitude, de 
et de m.
Pour t'aider un peu, voici une simulation faite avec des valeurs numériques arbitraires :
/m=10m/s2
vo=2m/s
xo=-1m
Un conseil concernant le portrait de phase : pense à la troisième équation caractéristique des mouvements rectiligne d'accélération constante :
v2-vo2=2a.(x-xo)
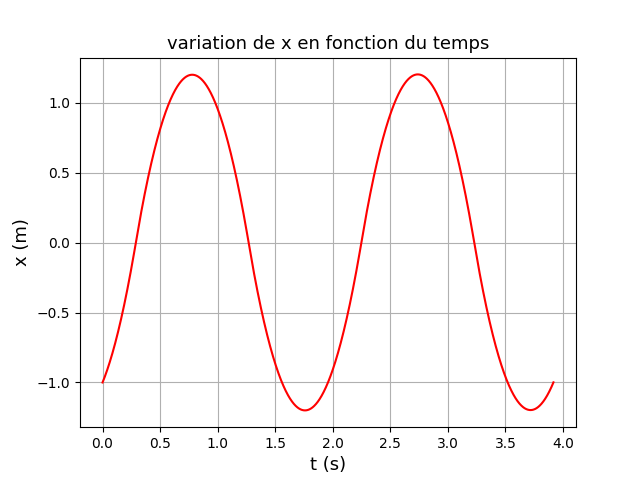
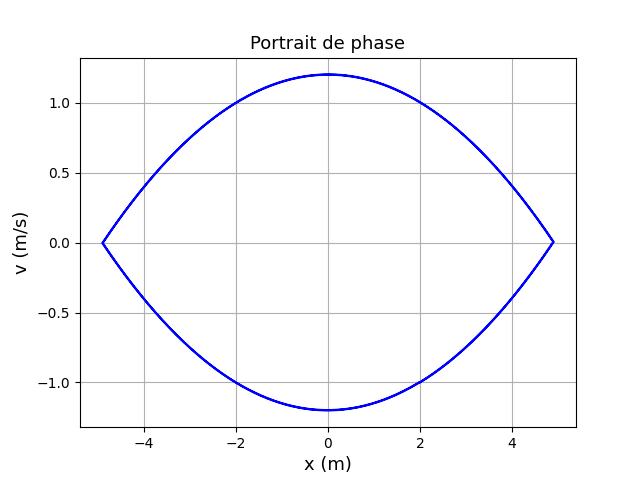
Je viens de m'apercevoir que j'ai permuté abscisse et vitesse dans le portrait de phase. Je rectifie.
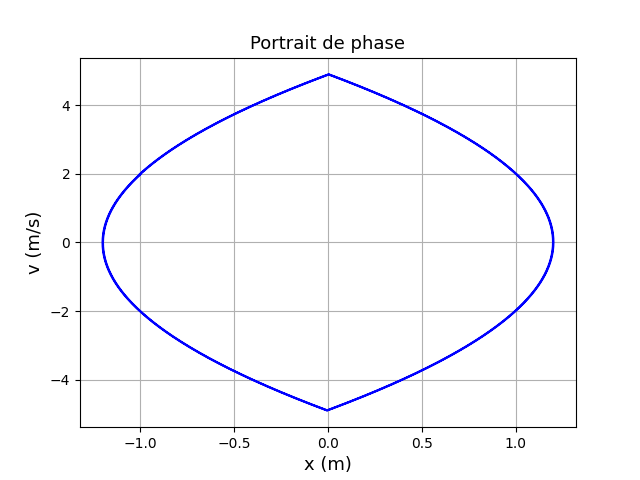
Salut, en fait j'ai repris mon calcul et il y a un problème.
la position initiale et la vitesse initiale. J'ai donc que
. Je cherche alors le premier instant
tel que
. J'obtiens
avec
défini dans mon message précédent. La particule a alors une vitesse
et se trouve en 0. On a alors
. On cherche alors la valeur d'annulation suivante de
qui se fait en
, ce qui pose problème dès lors que cette valeur peut être inférieure à
... Où est le problème?
Tu n'as pas tenu compte de mon conseil concernant la détermination préalable de l'amplitude xm des oscillations. Pour x=
xm, la vitesse s'annule. La conservation de l'énergie mécanique conduit pour ce cas particulier à :
Pour des raisons de symétrie, la durée pour passer de x=-xm à x=0 représente un quart de période. Sur ce trajet, le mouvement est uniformément accéléré d'accélération /m. En posant t'=0 en x=-xm, l'équation horaire sur ce trajet est, sachant que la vitesse est nulle en t'=0 :
t'=T/4 en x=0 :
Je te laisse finir le calcul...
Annuler
connectez vous