Inscription / Connexion Nouveau Sujet
Mouvement de particules chargees dans des champs ́electriq
Bonjour à tous,
J'ai besoin de l'aide pour un exercice de physique de PCSI , Merci
Enoncé:
On considère une particule de masse m de charge q. On la place dans les
champs uniforme
-> -> -> ->
E=E.ez et B=B.ey
. La particule est initialement en O avec
une vitesse nulle. On pose ωc = qB/m et on n2glige le poids.
Question:
1. Montrer que le vecteur vitesse a pour composantes : vx = (cos ωct−1) vy = 0
vz = sin(ωct)
Aide : Les deux ́equations vérifiées par vx et vy sont couplées, ce qui complique
la r ́esolution. On peut cependant se ramener `a une ́equation facilement soluble,
en effectuant la combinaison linéaire faisant apparaitre la grandeur complexe u =
vx + ivy, o`u i est le nombre complexe tel que i2 = −1. D ́eterminer l' ́equation
différentielle v ́erifiée par u et la résoudre, en faisant apparaˆıtre dans les calculs la
grandeur ωc = qB/m .
2. Quelle est la nature de la trajectoire obtenue ? La tracer approximativement
pour un électron puis pour un proton.
3. On définit A comme le point o`u z atteint son premier extremum. Déterminer
les coordonnées de A.
4. Cette fois-ci la vitesse initiale est selon Ox . Trouver une condition sur E et
B pour que le mouvement soit exclusivement selon Ox .
J'ai deja des élément de réponse pour la 1er question , Je pense que pour la deuxieme c'est un cycloîde. J'ai demander a mon professeur pour la 3eme , elle m'a parlé de dérivée nul à l'extremum et quil faut annulé les x je n'ai pas trop compris et la 4eme aucune idée.
Merci de bien voulair m'aider en image attaché on retrouve un shéma
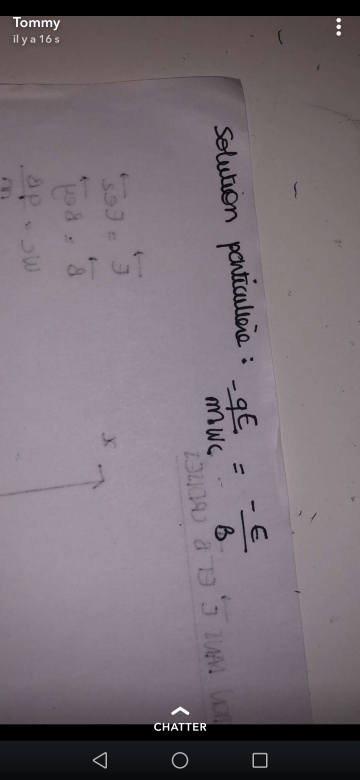

EDIT:
Bonjour,
J'ai réussis la premiere question et la deuxieme , il me faudrait juste de l'aide pour la deuxieme question s'il vous plait
Bonsoir
La trajectoire est effectivement une cycloïde. On trouve sur le net de nombreux corrigés de cet exercice.
Pour le point A, sommet de la cycloïde, tu peux effectivement étudier l'équation cartésienne de la trajectoire z=f(x) et considérer que la dérivée f'(x) s'annule au sommet. Il y a un peu plus simple sachant qu'à chaque instant le vecteur vitesse est tangent à la trajectoire : un sommet correspond nécessairement à vz(t)=0.
Pour la dernière question : suppose qu'à instant initial soit satisfaite la condition :
Il est facile de montrer qu'alors, le mouvement est rectiligne uniforme de vitesse .



