Inscription / Connexion Nouveau Sujet
Mouvement dans un champ électrique uniforme
Bonjour, voici mon exercice :
Dans un accélérateur linéaire de particules, un proton de charge e et de masse m = 1,7*10^-27 kg pénètre avec une vitesse initiale de valeur vo = 2,0*10^3 m.s-1, perpendiculaire aux armatures d'un condensateur plan. Dans ce condensateur règne un champ électrostatique uniforme de valeur E = 1,0 kV.m-1. Le poids du proton et l'action de l'air sont négligés. Sa vitesse finale doit être Vf = 2Vo
Charge élémentaire : e = 1,6*10-19C
intensité de pesanteur : g : 9,8 N/kg
1.Indiquer la polarité des plaques.
2.Quelles sont les caractéristiques de la force électrique F exercée sur le proton ?
3.Verifier que le poids peut-être négligé devant la force électrique.
4.Déterminer les coordonnées du vecteur accélération en fonction de e, E et m.
5.Quelle est la nature du mouvement du proton ?
6.Déterminer les coordonnées du vecteur vitesse et du vecteur position.
7.En déduire la distance d entre les armatures.
Je passe rapidement les réponses que j'ai fait :
1.plaque gauche positive et plaque droite négative car E est orienté du + vers le -.
2.F = qE
direction : celle de E
sens : celui de E
valeur Fe= eE
Fe = 1,6*10^16N
3.P = 1,7*10^-26N
P est environ 10 milliards de fois plus faible que Fe.
4. On applique la seconde loi de Newton. On est dans le référentiel terrestre supposée galiléen.
ma = Somme des forces
P négligeable, seule F est appliquée
a= eE/m
coordonnées de a :
x= eE/m
y = 0
5.a colineaire et de même sens que vo donc le proton a un mouvement rectiligne uniformément accéléré.
6. vx = (eE/m)*t + vo
vy = 0
vecteur position :
x = 1/2*(eE/m)t2 + vot
7.Je ne vois pas comment faire...
Il faut peut-être que (eE/m)*t = 2vo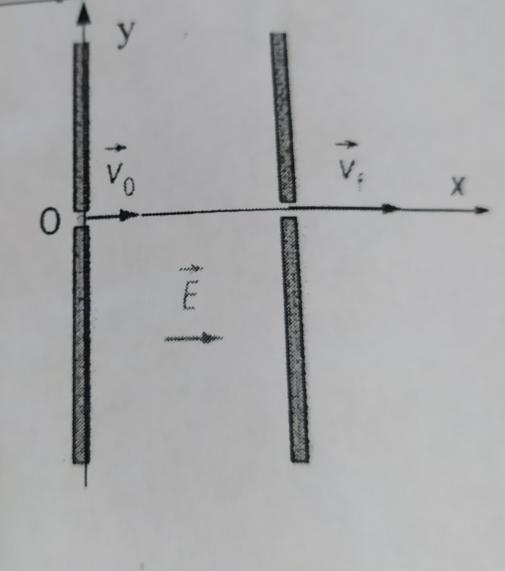
Question 7 :
Tu y es presque.
Le proton doit sortir du champ avec la vitesse 2v0
Cela se produit à la date t=
telle que :
2v0 =( eE/m) + v0
Tu tires de l'expression précédente.
A cette même date tu as x() = d
Tu en tireras " d " en fonction de m, V0, e et E
***Ce calcul numérique intermédiaire me semble superflu :
De 2v0 =( eE/m) + v0
on tire = m*v0 / (e*E)
qu'on injecte dans d = x( )
On obtient d = 3*m*(v0)² / (2 * e * E)
Ceci dit, le résultat numérique me laisse perplexe ....
qu'on injecte dans d = x(
)
On obtient d = 3*m*(v0)² / (2 * e * E)
Ca par contre j'ai pas compris...
d = x() = 1/2*(eE/m)² + vo
Je remplace dans la relation ci-dessus par m*v0 / (e*E) et j'obtiens après simplifications :
d = 3*m*(v0)² / (2 * e * E)
Puisque la question porte sur " d " et non sur " " il est inutile de calculer la valeur numérique de
Mais, comme indiqué précédemment, le résultat numérique obtenu pour " d " me laisse perplexe. Je te laisse le soin de faire le calcul et de me dire ce que tu en penses.
Mais moi j'aurais tout simplement mis à la place du t le résultat que j'ai trouvé au calcul précédent...
Quelle que soit la méthode utilisée le résultat devrait (évidemment 
) être le même.
Toutefois, tu auras du faire deux calculs numériques ( puis d ) là où je n'en fais qu'un seul :
d = 3*m*(v0)² / (2 * e * E)
donc une distance entre les plaques comprises entre 6 et 7 centièmes de mm, ce qui, comme je te le disais me laisse perplexe.
Mais quelle serait l'erreur alors ? Après je ne connais pas bien la taille des accélérateurs linéaires de particules...
Annuler
connectez vous