Inscription / Connexion Nouveau Sujet
Mouvement d'une particule
Bonjour j'ai un exercice que j'aimerais traiter mais j'arrive pas à démarrer. Pouvez vous m'aider s'il vous plait ?[rouge][/rouge]
On considère le mouvement d'une particule A, dans le repère R(O;ex;ey;ez) fixe, caractérisé par les équations cartésiennes paramétriques suivantes :
x(t) = a[wt-sin(wt)]
y(t) = a[1-cos(wt)]
z(t) = 0
w et t étant des constantes positives
1- Representer la trajectoire de la particule dans le plan xOy, wt appartient [-2pi,2pi]. Quelle est la nature de la courbe.
2-Donner les composantes cartésiennes du vecteur vitesse V de A par rapport à R du vecteur accélération a de A par rapport à R. En déduire leurs valeurs aux points de remboursement (wt=0 et 2pi). Commenter
3- Calculer la vitesse scalaire V. En déduire les accélérations tangentielle aT et normale aN ainsi que le rayon de la courbure R.
1)
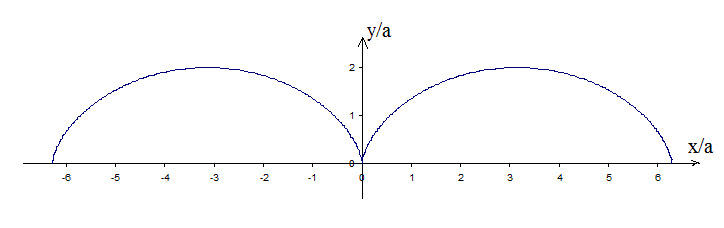
Et donc c'est une ...
-----
2)
Vx = dx/dt ...
Vy = dy/dt = ...
Vz = dz/dt = ...
d²x/dt² = ...
d²y/dt² = ...
d²z/dt² = ...
"points de remboursement" ... c'est plutôt : "points de rebroussement"
...
3)
v² = (Vx)² + (Vy)² + (Vz)² = ...
v = ...
Sauf distraction. 


