Inscription / Connexion Nouveau Sujet
Mouvement d'une bille dans une gouttière
Bonjour, je bloque sur un exercice.
Je sais que la bille glisse sans frottement et les equations paramétriques du mouvement sont :
x=R( +sin(
+sin( ))
))
z=R(1-cos( ))
))
Avec R=10 cm et g=10 m.s
Puis je dois exprimer la pente de la gouttière en fonction de R et  /2 en tout point M.
/2 en tout point M.
J'ai essayé de trouver l'équation de la trajectoire (z(x)) mais je n'arrive à rien. 
Merci d'avance 
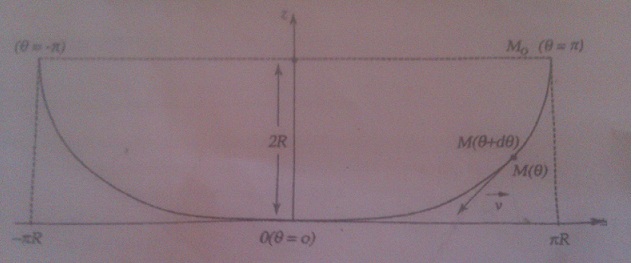
x=R(theta+sin(theta))
z=R(1-cos(theta))
dx/dtheta = R.(1 + cos(theta))
dz/dtheta = R.sin(theta)
dz/dx = (dz/dtheta)/(dx/dtheta)
dz/dx = sin(theta)/(1 + cos(theta))
dz/dx = tan(theta/2)
C'est la pente de la gouttière au point M repéré par l'angle theta.
-----
Sauf distraction. 
C'est d'accord, merci. 
Je dois maintenant calculer l'abscisse curviligne (toujours en fonction de R et theta/2) s(theta)=OM du point M.
On me propose de commencer par calculer ds=V(dx²+dz²) puis s=intégrale(ds).
Je n'avais encore jamais entendu parler d'abscisse curviligne donc je viens de me renseigner sur ce qu'était cet abscisse mais je ne vois pas comment résoudre cette question....
dx/dtheta = R.(1 + cos(theta))
dz/dtheta = R.sin(theta)
(dx/dtheta)² + (dz/dtheta)² = R².(1 + cos(theta))² + R².sin²(theta)
(dx/dtheta)² + (dz/dtheta)² = R².(1 + cos²(theta) + 2cos(theta) + sin²(theta))
(dx/dtheta)² + (dz/dtheta)² = 2R².(1 + cos(theta))
(dx/dtheta)² + (dz/dtheta)² = 2R².(2.cos²(theta/2) = 4R².cos²(theta/2)
V[(dx/dtheta)² + (dz/dtheta)²] = 2R.cos(theta/2)
L = S(de 0 à theta) [2R.cos(t/2)] dt
L = 4R.[sin(t/2)](de 0 à theta)
L = 4R.sin(theta/2)
C'est l'abscisse curviligne du point M correspondant à l'angle theta.
-----
Sauf distraction ou erreur. 
De toutes manières, ce type de calcul, sans savoir à quoi rime l'abscisse curviligne, ne sert à rien.


