Bonsoir
A priori, tes réponses sont correctes.

J'ai répondu en fonction des données de l'énoncé. La base doit être représentée sur cette figure.

On cherche maintenant à déterminer le temps qu'il faut entre le moment où l'objet est lâché (point A) et où il arrive au sol. Il faut exprimer Δt en fonction de h, g et l'angle .

Réponse : On a F=ma

Ici, Puz' et Nuz' se compensent. On a donc F=Pux' = mgsin(). Cela donne ma=mgsin(), soit a = gsin().

Si on note c la distance du plan incliné, on a c=h/sin().

On peut dire que c=1/2*a*(Δt)², soit h/sin()=1/2*(gsin())*(Δt)².

On se retrouve à la fin avec Δt=2h/gsin²().

Est-ce que ma démarche et l'expression finale sont correctes ?

OK. Tu peux éventuellement sortir le sinus au carré de la racine carrée.

On peut écrire t = (2h) / (sin()*g) ?

Maintenant, on cherche à expliquer pourquoi l'énergie mécanique du système est conservée et en déduire la vitesse en bas du plan incliné (point B).

Réponse : On a énergie mécanique = énergie cinétique + énergie potentielle.

Au point A, énergie cinétique = 0 et énergie potentielle = mgh.
Au point B, énergie cinétique = 1/2 mv²B et énergie potentielle = 0.

Conservation de l'énergie mécanique (car il n'y a que des forces conservatives qui agissent) :
énergie mécanique A = énergie mécanique B
mgh = 1/2 mv²B

En simplifiant, on obtient vB = 2gh.

Est-ce que l'expression de vB est correcte ?

Expression correcte. Préciser dans la solution que la seule force conservative susceptible de travailler est la force de pesanteur : la seule énergie potentielle prise en compte est ainsi l'énergie potentielle de pesanteur.

Après avoir atteint le sol, l'objet va suivre le chemin BCDEF. On néglige toujours les frottements.

Consigne : Faire le bilan des forces.

Réponse : On a la réaction normale N et le poids P.

Nu_r = Nu_r
Nu = 0

Pu_r = -mgsin()u_r
Pu = -mgcos()u

Donc N = Nu_r et P = -mgsin()u_r - mgcos()u

Est-ce que les projections des vecteurs sont correctes ?


PDF - 32 Ko

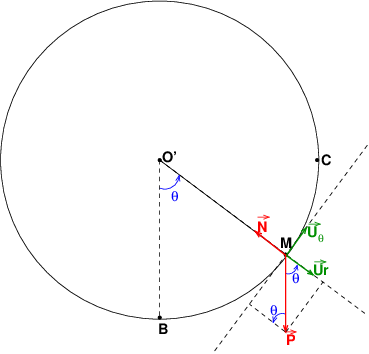
Il y a un problème au niveau de la figure de droite. O n'y désigne pas le centre de la trajectoire circulaire et la distance OM n'est pas égale au rayon R_o de la piste circulaire en tout point M.
N'ayant pas l'énoncé complet, difficile d'être formel sur la méthode la plus simple à adopter.
A priori, j'aurais tendance à choisir un repère d'origine O', d'axe (O'x) passant par C et d'axe (O'y) passant par D. L'angle polaire serait ainsi :


Il vaut -/2 en B, zéro en C et /2 en D.
Ta projection du vecteur devient alors correcte.
Pour la réaction de la piste : le petit solide qui glisse sur celle-ci est à l'intérieur de la piste, de sorte que le vecteur réaction normale , s'il existe, est nécessairement orienté de M vers O' :

Rectification :

Le schéma de droite ne fait pas partie de l'énoncé, c'est juste pour montrer comment j'ai placé les vecteurs u_r et u. Je viens de mettre un nouveau schéma qui présente la réaction normale et le poids. Mais le principe reste le même que dans le schéma de l'énoncé : un objet M qui suit un mouvement circulaire.

Pour la normale on a bien : N = -Nu_r

Pour le poids, est-ce qu'on a toujours P = -mgsin()u_r - mgcos()u ?


PDF - 34 Ko

Votre message précédent est juste, le schéma de l'énoncé montre qui part de B pour arriver à M, mais si on part de C pour arriver à M, cela ne change rien.

vanoise @ 28-02-2025 à 15:22

Rectification :

Concernant ton dernier fichier : la figure du bas est sans intérêt ; tu peux la supprimer. La figure du haut est correcte et très claire mais l'angle polaire y est défini différemment par rapport aux messages précédents. Les vecteurs force y sont correctement représentés mais il te faut revoir la projection du vecteur poids. Changer la définition de , modifie cette projection.

Si je place la base (u_r et u) sur le point M présent dans le schéma de l'énoncé (voir pièce-jointe de ce message) et que l'on garde comme l'angle partant de B pour aller à M, est-ce que la projection de P est : -mgsin()u_r - mgcos()u) ?


PDF - 14 Ko

La figure du haut, dans ton message de 15h24 et ta figure de 15h45 correspondent à la même définition de l'angle polaire . L'expression de en fonction de et de est donc la même dans les deux cas et ce n'est pas celle que tu proposes.
Seulement, sur la première figure : </2, sur la seconde : >/2;
je te conseille de faire tes projections à partir du cas </2 ; sinon, la trigonométrie peut être piégeante...

Ce schéma t'aidera peut-être. Restera ensuite à vérifier que le résultat est aussi valide pour >/2.

D'accord. Donc d'après votre schéma, on a mgcos()u_r - mgsin()u ?

Oui et cette relation est valide quelle que soit la position du point M sur la trajectoire circulaire.

Merci.

Maintenant, il faut établir les équations du mouvement dans la base polaire à partir de la 2ème loi de Newton.

On a F =ma avec a = -r²u_r + ru car on est dans un mouvement circulaire.

Donc on a - N + mgcos() - mgsin() = m*( -r²u_r + ru)

Pour la composante radiale, on se trouve avec N = mgcos()-mgsin()+mr².

Pour la composante tangentielle, on a r = -gsin().

Est-ce que tout cela vous semble correct ?

Je suis en train de revoir ce que j'ai écrit et je me suis trompé.

Pour la composante radiale on a N=mgcos()+mr².

Pour la composante tangentielle, on a r=-gsin().

D'accord pour :

Pour la norme de la réaction, vérifie bien les signes.
Indication pour la suite : tu peux remarquer :



et v² peux s'obtenir en fonction de v_B² et de par application du théorème de l'énergie cinétique.

Il faut maintenant écrire, en coordonnées polaires, l'expression de l'énergie mécanique du système lorsque l'objet est en mouvement circulaire.

Réponse : Em = Ec + Ep

Ec = 1/2mv² avec v=²+(r)², mais comme on est dans un mouvement circulaire, v=r.

Ep=mgh avec h=r(1-cos()).

Donc Em = 1/2mr² +mgr(1-cos())

Est-ce que cette expression est correcte ?

Expression correcte à une petite étourderie près : tu as oublié le carré pour la vitesse angulaire dans ta dernière formule. Il faut aussi préciser que tu as choisi l'altitude de B comme altitude d'énergie potentielle nulle.
Tu peux aussi remarquer que cette énergie mécanique vaut :

compte tenu des questions précédentes.

La question demande :
a) écrire, en coordonnées polaires, l'expression de l'énergie mécanique du système lorsque l'objet est en mouvement sur le cercle.
b) Que vaut cette énergie lorsque l'objet est au point B (juste avant que l'objet ne commence son looping) ?

Pour le a), on a bien Em=1/2mv² + mgh avec v=r donc Em = 1/2m(r)² + mgh ?

Pour le b), on a Em(B) = 1/2m(r)² ?

Tu n'as pas bien compris mes précédents messages, en particulier celui de 16h02 ...
Pour a) :



Pour b) :

Je n'ai pas compris pour le b).

Pourquoi Em = 1/2mv²B = mgh et non pas 1/2mv²B + mgh ?

Relis attentivement mon message de 16h02 : telle que tu as exprimé l'énergie potentielle de pesanteur à la question a), tu as choisis comme altitude d'énergie potentielle nulle, l'altitude de B. Donc, dans le cas particulier de la position B, l'énergie potentielle est nulle, l'énergie mécanique est simplement égale à l'énergie cinétique en B calculée aux questions précédentes.

Oui mais en bas du cercle, toute l'énergie mécanique est sous forme d'énergie cinétique car l'énergie potentielle est nulle. Au sommet du cercle, toute l'énergie mécanique est sous forme d'énergie potentielle, puisque la vitesse est nulle.

Alors pourquoi au point B, Em=1/2mv²B=mgh ?

On aurait Em=1/2mv²B en bas du cercle et Em=mgh en haut du cercle ?

Oui vous avez raison, je comprends mieux maintenant.

A partir des questions précédentes, il faut maintenant donner l'expression de la force de réaction normale exercée sur l'objet lorsqu'il tourne sur la boucle en fonction de 𝑚, 𝑔, 𝜃, 𝑅 et 𝑣𝐵.

Réponse : Lorsque l'objet est en bas de la boucle, Em=1/2mv²B=mgh et en tout point de la boucle, on a : Em = 1/2mr²²+mgr(1-cos())

Comme l'énergie mécanique est conservée, on a : 1/2mv²B=1/2mr²²+mgr(1-cos())

On note que la vitesse linéaire v de l'objet en tout point de la boucle est reliée par la vitesse angulaire par v=r.

On substitue cette expression dans l'expression de l'énergie mécanique : 1/2mv²B=1/2mr²²+mgr(1-cos()), soit 1/2mv²B=1/2mr²²+1/2m*2gr(1-cos()).

On obtient v²B=r²²+2gr(1-cos()), ce qui équivaut à v²=v²B-2gr(1-cos()).

On note maintenant que la force de réaction normale doit compenser l'accélération centripète et la composante radiale du poids.

La composante radiale de l'accélération est donnée par a=v²/r.

En tenant compte de la composante radiale de la force gravitationnelle, on a N-mgcos()=m*(v²/r), soit N-mgcos()=m*(v²B-2gr((1-cos))/r).

Est-ce que cette expression est correcte ?

Globalement d'accord avec ce que tu as écrit sauf cette phrase : « On note maintenant que la force de réaction normale doit compenser l'accélération centripète et la composante radiale du poids. ». Une force ne peut pas compenser une accélération : ce ne sont pas des grandeurs de même nature physique. La réaction normale exercée par la piste circulaire sur l'objet permet de maintenir la trajectoire circulaire ; son expression a été déterminée aux questions précédentes. Tes calculs me semblent corrects. Ils conduisent à :

Oui merci beaucoup.

Il faut maintenant en déduire la hauteur minimale h0 pour permettre à l'objet d'effectuer le tour de la boucle tout en restant en contact avec la piste.

Pour trouver la hauteur minimale, il faut s'assurer que la force de réaction normale reste positive ou nulle en tout point de la boucle.

Le point critique se trouve au sommet de la boucle, où =. En ce point, la force de réaction normale doit être au moins égal à 0 pour que l'objet reste en contact avec la piste.

On a alors : N=((mv²B)/r)+mg(3cos()-2). Sachant que cos()=-1, on a N=((mv²B)/r)-5mg.

Pour que N soit égal à 0 au sommet de la boucle, on a 0 = ((mv²B)/r)-5mg, soit v²B=5gr.

Pour déterminer la hauteur h0, on doit utiliser la conservation de l'énergie mécanique.
Em=1/2mv²B=mgh0.

Donc 1/2m(5gr)=mgh0, soit 5gr/2 = gh0, soit h0=5r/2.

Est-ce que tout ce que je viens d'écrire est correct ?

Il faut s'intéresser au point D car cette position correspond au minimum de N. Si ce minimum est positif, N sera positif en toute position. L'objet restera en contact avec la piste. D'accord avec tes calculs et ta conclusion.

On cherche maintenant à savoir si la vitesse au sommet de la boucle est nulle pour h=h0.

On peut dire que la vitesse au sommet de la boucle n'est pas nulle car l'objet doit maintenir une certaine vitesse pour fournir l'accélération centripète nécessaire afin de rester en contact avec la piste.

Si la vitesse était nulle, il perdrait ce contact et tomberait.

Est-ce que la justification est correcte ?

Ce que tu écris est correct. Il est possible d'être un peu plus précis en partant de l'expression générale de N déjà démontrée :



Au sommet D :



h=h_o est le cas particulier limite où la réaction N s'annule.

Donc, pour h=ho :

D'accord, merci beaucoup de m'avoir aidé pour toutes ces questions.