Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

mouvement d'un chasse neige

Posté par
mb89ma 19-06-09 à 12:45

Bonjour,
voila j'ai un exercice de mécanique des solides à résoudre.


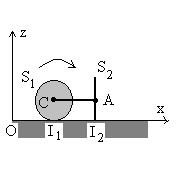
La figure schématise un chasse-neige se déplaçant sur une horizontale.
Ce chasse-neige est constitué d'une roue S1 (de centre d'inertie C, de rayon R, de masse m répartie uniformément sur la circonférence et de moment d'inertie J=mR2 par rapport à son axe) et d'une partie S2 (CABI2 ), indéformable de même masse m que la roue, de centre d'inertie A (on donne: CA = 2R; AI2 = R  ), en mouvement de translation parallèlement à l'axe Ox.
Le moteur exerce sur la roue un couple de moment C1\vec{y} (C1 constante positive, \vec{y} = \vec{z} ^ \vec{x}).
La roue tourne sans frottement autour de son axe (liaison pivot parfaite) et roule sans glisser sur le sol. On suppose que le coefficient de frottement de glissement f sur le sol est le même en I1 et en I2 (il vérifie ).
On note V\vec{x} la vitesse de C et \dot{\theta}

Question 1
Donner la forme du torseur cinématique associé à la roue S1.
Donner la forme du torseur cinématique associé à S2.

Question 2
Donner la forme des torseurs cinétique et dynamique associés à la roue S1.
Donner la forme des torseurs cinétique et dynamique associés à S2.

S'il vous plait, pourriez vous m'aider à résoudre ce problème.
J'ai fait le début de la question 1

\vec{V}(I1) = \vec{V}(C) + \vec{I1 C} ^ \vec\Omega
= V\vec{x} + R\vec{y} ^ \dot{\theta}\vec{y}
= (V - R\dot{\theta})\vec{x}

Pour S2 je n'arrive pas.
Merci à ceux qui pourront m'aider.

mouvement d\'un chasse neige

Posté par
mb89mare : mouvement d'un chasse neige 19-06-09 à 14:29


Je corrige
V\vec{x} + R\vec{z} ^ \dot{\theta}\vec{y}
= (V - R\dot{\theta})\vec{x}

J'ai cherché et voilà ce que j'ai trouvé :

Pour le torseur cinématique de S2 je trouve:
\vec{0}
V\vec{x}

Question 2

torseur cinétique associé à S1:
\vec{p}= m\vec{V(c)} = mV\vec{x}
\vec\sigma(c \epsilon S1)= Ic(\vec\Omega)=(mR2/2) \dot\theta\vec{y}

torseur dynamique associé à S1:
\vec{D(S1)}=m\dot{V}\vec{x}
\vec\delta(S1)=(mR2/2) \ddot\theta\vec{y}

torseur cinétique associé à S1:
\vec{p}=mV\vec{x}
\vec\sigma(c \epsilon S2)=\vec{0}

torseur dynamique associé à S1:
\vec{D(S2)}=m\dot{V}\vec{x}
\vec\delta(S1)=\vec{0}

Voila j'ai fait les deux premières questions et j'aimerais savoir si ce que j'ai fait est correct sinon veuillez m'indiquer mes erreurs.
Merci à tous ceux qui pourront m'aider.

Posté par
gbm Webmasterre : mouvement d'un chasse neige 19-06-09 à 14:39

Bonjour,

Question 1 :
TB !

Question 2 :
même si je vois où tu veux en venir il faut que tu expliques mieux ta démarche.

Posté par
mb89mare : mouvement d'un chasse neige 19-06-09 à 15:35

Pour le torseur cinétique de la roue S1:
d'abord je calcule la quantité de mouvement en appliquant directement la formule au point C.
Puis je calcule le moment cinétique de la roue en C, puisque ce point est le centre d'inertie de la roue.
Il suffit d'appliquer la formule du moment cinétique en C, je prends comme matrice d'inertie celle d'un cercle (je considère que le cylindre est d'épaisseur nulle).

Pour le torseur dynamique, il suffit de dériver le torseur cinétique de la roue S1.

Pour le torseur cinétique associé à S2:
Je calcule la quantité de mouvement grâce à la formule du cours.(p=mV)
Pour le moment cinétique, il faut considérer que le taux de rotation de S2 est nul, par conséquent son moment cinétique sera nul.
Pour le torseur dynamique je dérive le torseur cinétique, et je trouve également un moment dynamique nul.


Maintenant je voudrais de l'aide pour la question 3
On note G le centre d'inertie du système complet (de masse 2m), situé au centre du segment CA.
Quel est le moment dynamique en G de S1 et de S2?
Calculer le moment dynamique du système complet en G.

Pour la première partie de la question j'ai pensé à utiliser la règle des transports des moments.
Pour la deuxième partie de la question, je pense qu'il suffit de faire la somme des moments dynamiques de S1 et de S2 calculés en G.

Suis-je sur la bonne voie?

Posté par
gbm Webmasterre : mouvement d'un chasse neige 19-06-09 à 15:54

C'est bon.

Posté par
mb89mare : mouvement d'un chasse neige 19-06-09 à 16:55

question 3

moment dynamique de S1 en G:

\vec\delta(G\epsilon S1)=\vec\delta(C\epsilon S1)
= MR2\ddot{\theta}/2

Or M=2m donc:
=mR2\ddot{\theta}

\vec\delta(G\epsilon S2)= \vec{0}
car S2 est immobile dans le référentiel barycentrique.

donc au final on a:
\vec\delta(G)=\vec\delta(G\epsilon S1) +\vec\delta(G\epsilon S2)
=mR2\ddot{\theta}


Question 4
Ecrire la relation imposée par le roulement sans glissement en I1.
Utiliser cette relation pour exprimer les moments dynamique calculés précédemment en fonction de m, R et \dot{v}.

Relation sans glissement:
\vec{v}(I1\epsilonS1)
=(V-R\dot{\theta})\vec{x}
=\vec{0}

d'où V = R\dot{\theta}

Pour la deuxième partie de la question je bloque.
Pouvez-vous m'éclaircir svp.

Posté par
gbm Webmasterre : mouvement d'un chasse neige 19-06-09 à 17:14

Il n'y a pas de moment d'inertie /z pour le solide 2 ?

Posté par
gbm Webmasterre : mouvement d'un chasse neige 19-06-09 à 17:16

je te prépare un corrigé manuscrit.

Posté par
mb89mare : mouvement d'un chasse neige 19-06-09 à 17:45

merci
Voici le reste des questions
question 5
Appliquer au système complet, le théorème de la résultante dynamique et projeter l'équation obtenue sur les axes (x , z).

question 6
Appliquer au système complet, le théorème du moment dynamique en G.
En déduire une relation entre T1, T2, N1 et N2.

Question 7
Appliquer à la roue, le théorème du moment dnamique en C.
Exprimer T1 en fonction de C1, R, m et \dot{v}.

Question 8
Déduire de l'équation projetée sur l'axe Ox obtenue question 5 et l'équation obtenue question 6, une équation entre N1-N2 et m\dot{v}.
Grâce à l'équation projetée sur l'axe Oz obtenue question 5, déterminer N1 et N2 en fonction de m, g et \dot{v}.

Question 9
Le contact en I2 est tel que la relation suivante est vérifiée: -T2=k*N2.
Le contact en I1 est tel que la relation suivante est vérifiée: T1\lek*N1.
k est coefficient donné tel que 0.7 < k < 1 et les quantités -T2,T1,N2,N1sont supposées positives.
Montrer que T1=(2-3/2k)m\dot{v}+kmg.
En déduire l'expression de \dot{v} en fonction des données m,g,R,k et C1.
Achever la détermination de N1,N2,T1 et T2 en onction exclusivement des données du problème.

Question 10
Quelles conditions doit vérifier le couple C1 pour que le mouvement déterminé ci-dessus soit effectivement réalisé lorsque le mouvement du chasse neige se fait sans accélération, c'est à dire à vitesse constante?

Merci beaucoup pour ton aide précieuse.

Posté par
gbm Webmasterre : mouvement d'un chasse neige 19-06-09 à 17:49

Tu vas me démoraliser avec cet exo long !!!

Posté par
mb89mare : mouvement d'un chasse neige 19-06-09 à 17:57

J'essaie de le faire quand même, je suis pas comme certains qui te balancent l'exo et attendent.
Merci encore une fois pour ton aide.

Posté par
gbm Webmasterre : mouvement d'un chasse neige 19-06-09 à 18:01

Aïe ! Je ne peux pas envoyer de mail à destination des boîtes MSN... As-tu une autre adresse mail ?

Posté par
mb89mare : mouvement d'un chasse neige 19-06-09 à 19:09

oui:

mbodouche@gmail.com

Merci encore une fois.

Posté par
gbm Webmasterre : mouvement d'un chasse neige 19-06-09 à 19:15

voila


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2024

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !