Réponse:
1) calcul de la vitesse angulaire et de la période de chaque cycliste
La longueur de la circonférence est



Par définition =

Soit

Et

De même, par définition la période d'un mouvement circulaire uniforme est

Donc T₁ = 25/3 secondes

Et  T₂ = 20/3 secondes.

Pour la 2) question, j'avoue que je n'arrive même pas à commencer

Bonjour,

Question 1 :  OK

Question 2 :
Pour commencer ....
A l'instant où M2 rejoint M1 pour la première fois il a effectué 1 tour de plus que lui.
En jargon cycliste on dit que M2 "a pris 1 tour" à M1

Donc, si je comprend bien, je calcule la durée du 1er rattrapage, c'est ça ?

Soit t₁ la durée du 1er rattrapage :
Les équations horaires sont :
S₁ = V₁t₁  et
S₂ = V₂t₁

Mais puisque M₂ a pris 1 tour à M₁, alors S₂=L+S₁  Où L = 100 m est la longueur de la circonférence.

Donc L+S₁=V₂t₁
En remplaçant S₁ par son expression et en tirant t₁, on obtient :
t₁=L/(V₂-V₁)=100/(15-12)
Soit t₁=100/3 secondes

Je fais la même chose pour le 2e rattrapage, sachant que M₂ a pris 2 tours à M₁, je trouve la durée du 2e rattrapage t₂= 2*100/3 secondes

3e rattrapage, je trouve t₃=3*100/3 secondes

Ainsi de suite jusqu'au nième rattrapage, je trouve t_n=n*100/3 secondes,  avec n le nombres de tours effectués par M₂.

Ces durées forment une progression arithmétique de raison T=100/3 secondes.
D'où M₂ rattrape M₁ à intervalles de temps réguliers T=100/3 secondes.

C'est ça ??

Salut,

Moi j'ai obtenu la même réponse que toi mais différemment.

La vitesse relative de M2 par rapport à M1 = (15/50 - 12/50) rad/s = 3/50 rad/s

(En gros, je fais comme si M1 était immobile)

Ensuite je calcule la période de M2 avec cette vitesse relative (càd toutes les fois où il passe à côté de M1), ce qui donne :

(2 rad)/((3/50)rad/s) = 100/3 s

Je suppose que si on a obtenu la même réponse avec 2 méthodes différentes, c'est que c'est la bonne réponse.

Il existe en effet bien des manières pour obtenir la solution.
En voici une autre :
Chaque seconde M2 prend 15 - 12 = 3m d'avance sur M1
Pour prendre un tour soit 100m d'avance il faudra donc (100/3) =33,3s

Toutes les 33,3s M2 rejoint M1

Toujours question 2)
On demande le nombre de tours effectués par chacun des deux mobiles durant l'un de ces intervalles.
Là je suis bloqué !!!

Là il me semble que le raisonnement est simplement de trouver la distance parcourue en un certain intervalle de temps (ici 100/3 secondes), puis de voir combien de fois une distance donnée (1 tour = 100 m) est parcourue durant cet intervalle de temps.

Je ne sais pas si ça te met sur la piste...

Je pense qu'il n'est pas très efficace d'avoir deux personnes différentes ayant chacune leur propre méthode pour aider hdiallo.

Je laisse donc bien volontiers Prigogine gérer la suite de ce exercice.

Ouh, je vais tenter de me montrer digne de cette assignation. En espérant que hdiallo n'ait pas perdu son meilleur professeur

Par exemple, lors du 1er intervalle de temps, la distance parcourue par M₂ est :
D = L+S₁=L+V₁T=100+12*100/3=500m
Ensuite je passe par la règle de trois :
1 tour --------> 100 m
n tours <------500 m
Soit n = 5 tours (pour M₂ pendant le 1er intervalle de temps)

Je fais la même chose pour M₁, c'est ça ?

Oui, ça fonctionne. J'ai obtenu la même réponse.

Après je crois que tu peux faire plus simple en posant une équation du genre:

nbr de tours en un temps T = (vitesse . T)/longueur d'un tour

ou avec la vitesse angulaire

nbr de tours en un temps T = (vitesse angulaire . T)/2

Question 3
Il s'agit d'un croisement. La somme des distances parcourues par M₁ et M₂ lors du 1er croisement est égale au périmètre L du cercle. La durée du 1er croisement constitue la période, car les vitesses sont constantes.
Donc je fais L=(V₁+V₂)T
Soit T=L/(V1+V2) = 100/(12+13)
Soit T=4 s
Le 1er croisement dure t = T=4 s
Le 2e croisement  dure t =2*T = 8 s
Ainsi de suite, le nième croisement durera t = n* T

C'est ça ??

Salut hdiallo,

T'as fais une petite erreur d'inattention si je me trompe pas, c'est 100/(12+15), mais de toute façon c'est pas très grave.

Et puis je ne suis pas sûr que la suite de ce que tu as écris soit utile pour ton exercice.

Comme tu l'as écrit : "La durée du 1er croisement constitue la période, car les vitesses sont constantes." Ce que tu dis après, c'est que les cyclistes se recroisent toutes les n périodes, et que le nième croisement arrivera à la nième période après le départ des cyclistes. Donc en fait tu donnes juste une info évidente qui n'est pas demandée.

L'exercice te demande la position des cyclistes à chaque période, avec A étant la position de départ des deux cyclistes. Si on réfléchit en position angulaire, on pas par exemple dire que A = 0 radians. Ensuite, une deuxième chose dont il faut tenir compte, c'est que les cyclistes roulent en sens inverse. Donc il y en a un dont la vitesse angulaire sera négative, et l'autre dont la vitesse angulaire sera positive, et donc il y en aura un dont la position sera négative, et l'autre dont la position sera positive (en effet on peut avoir des mesures d'angles négatives, dessine un cercle pour te représenter la situation si tu ne l'as pas déjà fait).

A partir de là, la question que tu dois te poser c'est : qu'elle est la position de chaque cycliste au moment où ils se croisent, càd après une première période. Ensuite, la vitesse est constante, donc la position de chaque cycliste devrait être le produit de la vitesse par le nombre de période (Position = vitesse . temps), ou simplement la position B (leur position après le premier croisement) multipliée par le nombre de périodes.

De là, la dernière question que l'exercice te pose, c'est de voir s'il y a un multiple de la période pour lequel les deux cyclistes reviennent en position A. Je crois que le mieux pour résoudre ce problème, c'est de penser avec les radians. Quelles données as-tu ? Ils sont sur un cercle, ils partent du même point, ils vont en sens inverse, ils ont une vitesse constante. Comment tu traduis en terme de radians le fait qu'ils reviennent chacun en position A ?

Salut Prigogine,
Je rectifie d'abord mon erreur de 100/(12+13).

Êtes-vous d'accord avec moi que la période de leur différentes rencontres est T = 100/(12+15) secondes ?

Oui, je suis d'accord avec vous, je fais la même chose.

Maintenant, calculons les positions B,C,D...de ces rencontres.
Soit A leur position initiale (c'est à dire à t=0)
Le 1er croisement a lieu en B, après une durée t=T=100/27 s.
Supposons que M₁ suit le sens positif de la trajectoire orientée, M₂ le sens négatif.
L'abscisse curviligne de B est S_B=V₁T=12*100/27=44,4 m
L'abscisse angulaire correspondante est

C'est ça ?

Si ma réponse est vraie, existe-t-il une autre méthode plus simple ??

non ça me semble correct, j'obtiens les mêmes réponses avec la même méthode. Du coup il faut continuer, donner les positions suivantes, et puis les positions du deuxième cycliste. Et enfin le moment où ils se retrouvent en A.

Croisement en C:
S_C=V₁(2T)=12*2*100/27=88,8 m
L'abscisse angulaire correspondante est :


Croisement en D:
S_D=V₁(3T)=12*3*100/27= 133,2 m
L'abscisse angulaire correspondante est :

Soit E la position du 4ème croisement :
S_E=4*S_B=4*44,4=176,6m

Soit F la position du 5ème croisement :
S_F=5*S_B=5*44,4=222m

les positionsdu 2ème cycliste sont:
S_2B=V₂T=15*100/27=55,5m

S_2C=2*S_2B=111,1m

S_2D=3*S_2B=166,7m

S_2E=4*S_2B=222m

S_2F=5*S_2B=277,5m

Finalement, j'ai choisi d'utiliser les abscisses curvilignes pour trouver les positions de leur différentes rencontres.
Je constate que S_1F=_2E=222m

Comment calculer le nombre de périodes T au bout duquel M1 et M2 se retrouvent simultanément en A ?
Je suis confus là !!

Heu alors, déjà pour être tout à fait honnête, je ne maîtrise pas bien le concept d'abscisse curviligne, donc je ne peux pas dire si tu l'utilises bien, il faudrait demander à quelqu'un de plus calé que moi.

Mais déjà il me semble qu'il y a un problème qui est que tes calculs de positions ne tiennent pas compte du fait que les cyclistes vont en sens inverse.

Et puis il me semble aussi que tes mesures d'abscisses angulaires sont erronées, parce que R = 50/ et non 100

Perso je te conseil (humblement) de modéliser la situation en faisant un dessin, et puis je t'encourage aussi à utiliser l'abscisse angulaire, et puis je t'encourage aussi à écrire tes radians comme des multiples de , je crois que ça t'aidera à réfléchir.

Il me semble qu'ici la question à se poser c'est : que veut dire que M1 et M2 se retrouvent en A, qui est leur position de départ, compte tenu du fait que leur mouvement est circulaire. Comment exprimerais-tu en radian le fait que M1 et M2 soient revenus en A ?

Bon après tu peux réfléchir en abscisses curvilignes, mais de nouveau il me semble qu'il faut tenir compte du fait que M1 et M2 vont en sens inverse. Et du coup de nouveau, la question est de se demander comment traduire mathématiquement le fait que M1 et M2 soient revenus en position A, qui est leur position de départ sur une trajectoire circulaire qui fait 100m.

Merci prigogine.

Sollicitons quelqu'un pour nous appuyer.

Bon, je reviens mettre mon grain de sel ....
Je suis d'accord avec Prigogine pour
- Faire un schéma
- Utiliser plutôt les abscisses angulaires que les abscisses curvilignes.
- Privilégier la mesure des angles en multiples de π

Question 3 :
T = (100/27)s             OK
On recherche les positions des rencontres B,C,D etc ...
Abscisse angulaire du cycliste M1 ( en radian )
Pour la 1ère rencontre : α₁ = ω₁ * T = (6π/25) * (100/27) = 8π/9 rad
Donc rencontres en B, C, D, E  .......  aux abscisses angulaires 8π/9  ;  16π/9  ;  6π/9   ;  14π/9 .... rad

Pour le cycliste M2 même méthode avec ω₂ = - 10π/9 rad/s

Résultats rassemblés ci-dessous sous forme de schémas.

Conseil : Ne pas confondre les abscisses de position (comprises entre 0 et 2π) avec les angles balayés par les cyclistes (qui deviennent vite supérieurs à 2π) cela facilite le calcul du nombre de périodes et les distances parcourues par les deux cyclistes pour se retrouver en A

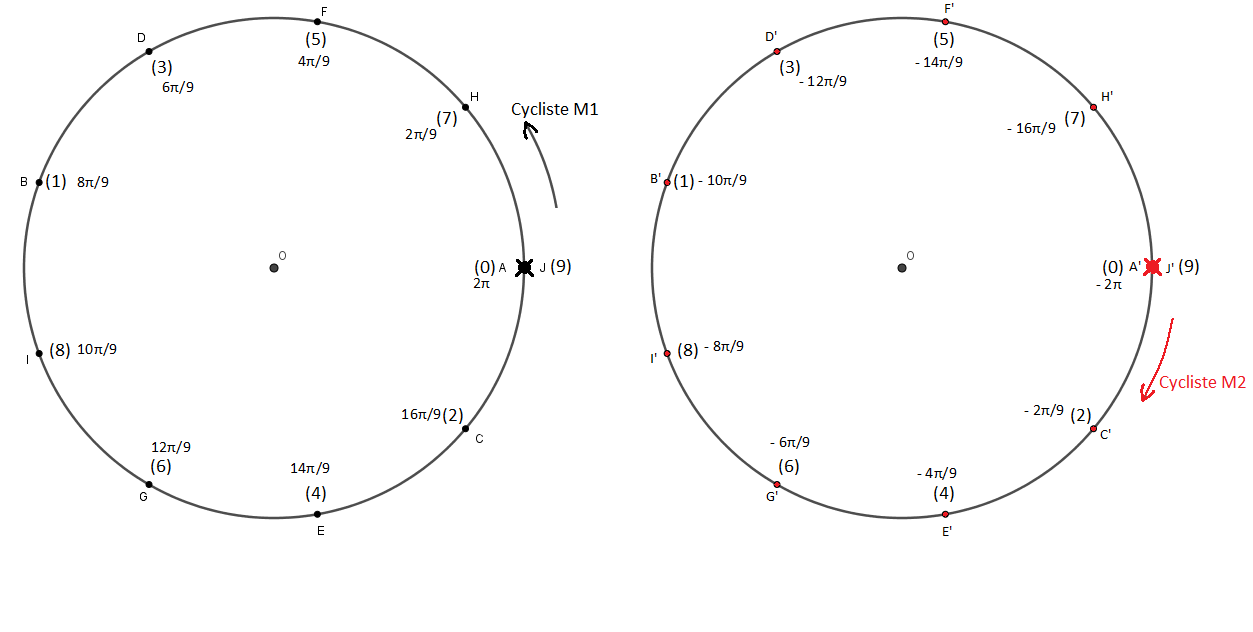
Merci odbugt1 !

Ce que je ne comprend pas, ce sont les valeurs , etc...

Sinon quand j'applique la relation je trouve au lieu de , et au lieu de , etc...

24π/9 est l'angle parcouru (ou balayé) par M1 à la date t=3T
En d'autres termes cet angle balayé est tel que :
24π/9 = 6π/9  + 18π/9 =  6π/9  + 2π  = 1 tour + 6π/9

6π/9 ( ou mieux  2π/3 ) est l'abscisse angulaire (donc la position) de M1 à la date t=3T

J'ai compris.
Maintenant, au bout de combien de périodes se retrouvent-ils simultanément en A ?
Sur la figure, j'ai l'impression que c'est au bout de 9 périodes.
Mais je ne sais pas comment trouver 9 à travers une équation.

Pour M1 :
L'angle "élémentaire" correspondant à une période de M1 est égal à 8π/9
Soit "k" le nombre de périodes nécessaire pour que les deux cyclistes se retrouvent en A
M1 doit parcourir un angle égal à 8kπ/9  ( avec k entier positif )

Soit K le nombre entier de tours effectué par M1 pour rencontrer M2 en A
M1 doit parcourir un angle égal à 2Kπ

On a donc :
8kπ/9 = 2Kπ
donc k / K = 9 / 4
k et K étant des nombres entiers on en déduit,  pour un premier passage simultané en A, que  la solution est la plus simple possible soit k = 9  et  K=4
M1 parcourt 9 angles élémentaires et effectue 4 tours pour retrouver M2 en A

Raisonnement analogue pour M2 facilité parle fait que pour lui aussi k=9

Merci odbugt1.
Maintenant, pour la distance qu'ils ont parcouru au bout de 9 périodes, je fais :
Pour M1 :


Pour M2 :
Je fais

C'est ça ??

Les distances parcourues s'expriment en unités de longueur.
On a montré que M1 a tourné d'un angle de 4 tours pour se retrouver en A en même temps que M2
Il a donc parcouru 4 * 100 = 400m

Pour M2 :
|ω₂| =  3π/10 rad/s
T = (100/27)s
Pour la première rencontre M2 a tourné (dans le sens inverse de M1) d'un angle  
α₂ = ω₂ * T = (3π/10) * (100/27) = 10π/9 rad
La rencontre en A se produit au bout de 9 périodes :
M2 a tourné d'un angle 9 * 10π/9 rad = 10π radians soit 5 tours
Il a parcouru 5 * 100 = 500m

Merci odbugt1
Merci  Prigogine

J'ai encore manqué du bon sens.

Merci à vous tous

Attention dans mon message du 09-11-21 à 23h46 j'ai écrit par erreur :

"Pour le cycliste M2 même méthode avec ω₂ = - 10π/9 rad/s "
alors que j"aurai du écrire :
"Pour le cycliste M2 même méthode avec ω₂ = - 3π/10 rad/s "

Comme il s'agit d'une simple erreur de frappe cela ne change rien à la suite.

D'accord, j'ai même pas pu remarquer cela

De toutes les façons beaucoup