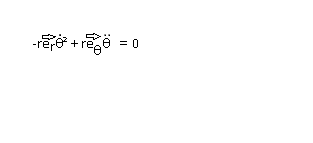Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths supForum Supérieur de maths sup PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths sup
Partager :

Mouvement circulaire

Posté par
drohan 23-12-11 à 19:47

Bonjour,
Étant donné que nous venons de commencer la mécanique je n'arrive pas à écrire l'équation différentielle d'un point matériel quelconque sur un rail circulaire.

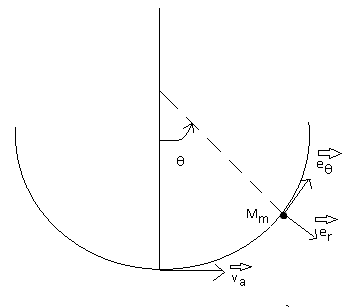
Enoncé : Un petit objet assimilé à un point matériel M, de masse m, peut glisser sans frottement le long d'un rail ayant la forme d'un demi-cercle de centre O de rayon R placé dans un plan vertical.
Le rail est fixe par rapport au référentiel terrestre galiléen.
A l'instant t=0, l'objet est lancé du point Mo (Le point Mo se situe à l'intersection entre la normale et le rail) avec une vitesse Vo.

Mouvement circulaire

Posté par
drohanre : Mouvement circulaire 23-12-11 à 19:48

J'ai réussi à trouver quelque chose en faite mais je ne sais pas me débarrasser du vecteur RN

Posté par
drohanre : Mouvement circulaire 23-12-11 à 19:49

Désolé j'ai oublié d'insérer la pièce jointe

Mouvement circulaire

Posté par
athrunre : Mouvement circulaire 23-12-11 à 20:33

Bonsoir,

puisque \vec{R_N} est normale, sa composante selon \vec{e_\theta} est nulle, donc projette ton équation sur \vec{e_\theta}.

D'ailleurs il y a une faute dans une de tes formules :

\blue\Large m\vec{a}=m\left(-R\dot{\theta}^2\vec{e_r}+R\red{\ddot{\theta}}\blue\vec{e_\theta}\right)

Posté par
drohanre : Mouvement circulaire 23-12-11 à 20:47

Oui mais du coup j'ai encore une expression de RT qui se "ballade" toujours ^^

Posté par
athrunre : Mouvement circulaire 23-12-11 à 20:51

C'est quoi R_T ?

Posté par
drohanre : Mouvement circulaire 23-12-11 à 21:13

Une des composantes de la réaction du support non ?

Posté par
athrunre : Mouvement circulaire 23-12-11 à 21:18

Ah la réaction tangentielle tu veux dire ! Eh ben en fait y en a pas puisqu'il n'y a pas de frottements !

Posté par
drohanre : Mouvement circulaire 23-12-11 à 21:29

Ah oui d'accord, je suis con Merci beaucoup.
Au final je trouve alors :

Mouvement circulaire

Posté par
athrunre : Mouvement circulaire 23-12-11 à 21:58

ben non ...

reprends la deuxième équation de ton message de 19:49 et projette-là sur \vec{e_\theta}

Posté par
drohanre : Mouvement circulaire 23-12-11 à 22:02

D'accord,

Mouvement circulaire

Posté par
athrunre : Mouvement circulaire 23-12-11 à 22:08

voilà ! il y a juste une erreur de signe c'est :

mR\ddot{\theta}=-mg\sin \theta

Donc on a :

\blue\Large\boxed{\ddot{\theta}+\frac{g}{R}\sin \theta=0}

Posté par
drohanre : Mouvement circulaire 23-12-11 à 22:13

Ah oui :s j'ai quelques soucis en mathématique et en physique en ce moment, vous m'avez bien aidé merci. Si vous avez besoin de quelque chose =)

Posté par
athrunre : Mouvement circulaire 23-12-11 à 22:23

pas de soucis

une remarque :

a) si tu étudies les petites oscillations c'est-à-dire si \theta_0 l'angle initial est petit et que la vitesse initiale est nulle, tu peux faire l'approximation (développement limité du 1er ordre) \sin \theta\approx\theta et ton équation devient :

\ddot{\theta}+\omega_0^2\theta=0 où \omega_0=\sqrt{\frac{g}{R}} est la pulsation propre. C'est l'équation d'un oscillateur harmonique. L'équation du mouvement est une équation linéaire du second ordre à coefficients constants que tu sais résoudre. La solution générale est de la forme \theta(t)=A\cos(\omega_0t)+B\sin(\omega_0t) où A et B sont des constantes que tu détermines avec les conditions initiales.

b) ici dans le cas général (c'est-à-dire même si les oscillations sont pas petites) tu peux obtenir l'inégrale première du mouvement : qui porte son nom car c'est l'équation obtenue après avoir intégré une fois l'équation du mouvement par rapport au temps. Ici l'astuce classique consiste à multiplier chaque membre de l'équation du mouvement par \dot{\theta} :

\dot{\theta}\ddot{\theta}+\omega_0^2\dot{\theta}\sin \theta=0 que tu intègres en :

\Large\frac{1}{2}\dot{\theta}^2-\omega_0^2\cos \theta=\text{constante}, la constante tu la détermines encore avec les conditions initiales.

Posté par
drohanre : Mouvement circulaire 30-12-11 à 12:52

En faite je voudrais revenir sur ta remarque a), car tu as bien vue les choses puisque dans la suite de l'exercice il suppose que V0 est suffisamment faible pour que << 1 rad.
Il faut que je détermine alors l'expression de en fonction de V0,g,R et t. Le souci c'est que je n'arrive pas à déterminer A et B.

Posté par
drohanre : Mouvement circulaire 30-12-11 à 17:40

up

Posté par
athrunre : Mouvement circulaire 30-12-11 à 23:33

Que valent et \dot{\theta} à t=0 ?

Posté par
athrunre : Mouvement circulaire 02-01-12 à 15:41

A t=0 on a :

\theta=\theta_0\ \text{et}\ \dot{\theta}=\frac{v_0}{R}.

\theta(t)=A\cos(w_0t)+Bsin(w_0t) \\ \theta(0)=A=\theta_0 \\ \dot{\theta}(0)=Bw_0=\frac{v_0}{R}

donc A=\theta_0\ \text{et}\ B=\frac{v_0}{Rw_0}.

\Large\blue\boxed{\boxed{\theta(t)=\theta_0\cos(w_0t)+\frac{v_0}{Rw_0}\sin(w_0t)}}


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !