Inscription / Connexion Nouveau Sujet
mouvement avec frottement fluide
salut mes amis
j'ai besoin un aide pour un problème :
un corps s considéré comme un point matériel est lancé vers le haut a partir d'un à partir d'un point A situé a du sol avec une vitesse initiale
on suppose que l'aire applique sur le corps un force de frottement
1- Établir l'équation différentielle du mouvement
2- donner l'équation horaire de mouvement
2-Quelle est la hauteur maximale atteinte par le corps ?
pour la 1ère question on a :
la projection sur Oz nous donne :
ce qui donne:
c'est une équation non linéaire, donc je ne sais pas s'il admet une solution
pour la 3ème question
le théoreme de l'energie cinetique
et je me bloque
C'est à la troisième question que la méthode déjà étudiée peut s'appliquer. Pour l'équation horaire, il faut séparer les variables :
Il suffit d'intégrer à gauche par rapport à v et à droite par rapport à t. Tu obtiens le résultat à une constante près puisque les primitives ne sont définies qu'à une constante additive près ; constante que tu obtiens à partir des conditions initiales. Indication d'ordre mathématique :
avec a et b : deux réels positifs :
La méthode de mon message de 18h23 permet d'exprimer t en fonction de v assez simplement mais exprimer v en fonction de t se complique dans la mesure où la vitesse initiale n'est pas nulle. Quant à intégrer pour avoir x en fonction de t...
Je serais curieux de savoir d'où vient ce problème. Celui de la chute verticale avec frottement en est beaucoup plus simple dans la mesure où il est possible de poser de façon réaliste vo=0. Pas possible évidemment d'avoir une vitesse nulle pour un lancer vers le haut.
En revanche, avec cet énoncé, exprimer v2 en fonction de z en utilisant la méthode étudiée dans ton message précédent est tout à fait possible et permet d'obtenir l'altitude maximale atteinte.
Bon journée Vanoise,
Merci pour votre aide;
en ce qui concerne votre dernière remarque, c'est vrai que le chute libre sans vitesse initial est plus simple, mais il y en a de nombreux problème qui propose un chute libre avec une vitesse initiale, un exemple simple est le sujet suivi par toi dans notre forum![]() Mecanique
Mecanique
(J'essayer de traiter ce sujet ultérieurement puisque c'est un bon exercice pour maîtriser les problèmes des forces de frottement)
pour votre indication de calquer les traitements concerne le pendule sur notre problème
j'ai jamais penser à ça, c'est une excellente idée
je procède comme suit :
posons
on obtient :
équation linéaire a pour solution (si je ne trompe pas)
la constante A se déterminer par les condition initiale:
à t=0 , et
si on utilise la méthode mentionné dans votre message
on obtient
posons
donc
v=\sqrt{\frac{mg}{k}}.tg(\sqrt{\frac{kg}{m}}(N_0-t))
et et
donc
Je réponds pour l'instant à ton message du 06-02-21 à 10:14. Je répondrai plus tard à ton message du 06-02-21 à 10:16.
De très bonnes choses et quelques grosses erreurs... Je reprends pas à pas :
Attention : étourderie sans doute : sous Tex, on obtient une fraction avec « \frac » et non « \fract ». Cela dénature évidemment ton équation différentielle. Tu as aussi oublié un « u ». L'équation différentielle s'écrit en fait :
Solution générale :
Pour simplifier, je choisis l'origine du repère confondu avec la position d'équilibre : zo=0, donc :
Tu as commis une étourderie dans l'expression de A ; tu aurais pu t'en apercevoir très simplement en vérifiant l'homogénéité de ta formule ; on ne peut additionner ou soustraire que des grandeurs de même dimension physique : additionner vo à 2g est nécessairement faux. Cette remarque très générale permet d'éviter bien des erreurs ou étourderies.
L'expression de u=v2 permet simplement d'obtenir l'altitude maximale zm : c'est la valeur de z pour laquelle u=0.
Je réponds à ton message du 06-02-21 à 10:16. La méthode me semble correcte mais j'ai repéré quelques erreurs ou étourderies au niveau des manipulations des constantes m, k et g. Étourderie peut-être : l'équation à intégrer est :
Plutôt que No, je note tm la date correspondant à l'altitude maximale atteinte donc à une vitesse nulle :
La méthode que tu utilises pour obtenir l'équation horaire est bonne mais les confusions précédentes se répercutent... J'obtiens, toujours en posant z=0 en t=0 :
J'ai vérifié que ces équations sont en accord avec une simulation informatique mais je ne suis pas à l'abri d'une erreur de retranscription avec l'éditeur d'équations...
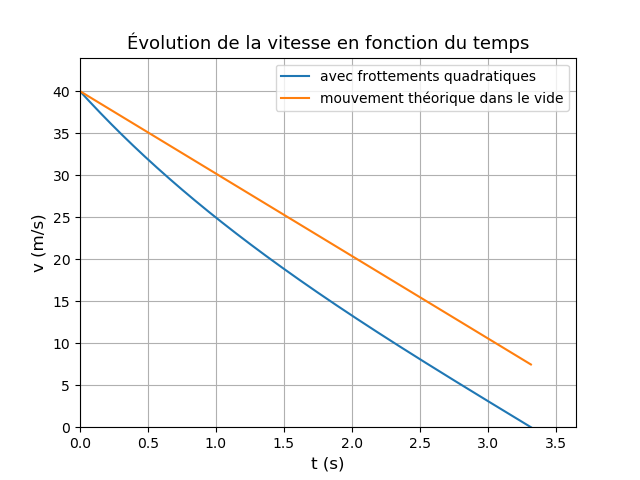
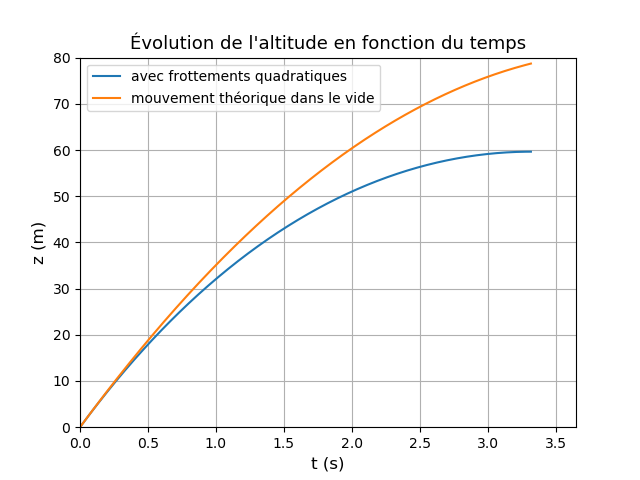
Pour illustrer mes deux précédents messages, voici les simulations correspondants aux conditions initiales suivantes :
zo = 0 ; vo = 40m/s ; (k/m)=5.10-3m-1 ; g=9,81m/s2 .
Ces valeurs conduisent à :
zm = 59,6m ; tm = 3,32s
Je te laisse interpréter l'allure de ces courbes.
salut Vanoise,
merci pour votre correction,
j'ai commis beaucoup des fautes soit de tapage soit de calcul, mais en générale la difficulté est surpassé et le problème est résolu, c'est pas comme au début ou je ne sais pas de quoi commencer
merci
on peut reformuler l'expression de z
on a:
ce qui donne :
or:
ce qui donne :
a t= t_m la vitesse s'annule est le corps atteind l'alltitude maximale z_m
avec :
résultat compatible avec la méthode suivi dans le message 06-02-21 à 12:59
on a
à on a
pour le commentaire des graphe:
mouvement sans frottement :
la variation de la vitesse : elle décroit linéairement
on a
l'amplitude est un parabole
mouvement avec frottement :
la variation de la vitesse : elle décroit tangentiellement
l'amplitude il croit d'une manière logarithmique
D'accord avec tes résultats. Juste une étourderie de signe à la dernière ligne de ton message du 08-02-21 à 15:36.
Concernant la courbe de vitesse : on peut aussi remarquer que la courbe réelle s'écarte assez rapidement de la courbe correspondant au vide pendant la première seconde du mouvement : logique : c'est dans cette première phase que la vitesse est la plus importante, donc que les frottements ont le plus d'influence. Inversement, pour t>2s, la courbe se confond pratiquement avec un segment de droite parallèle à la droite correspondant au vide ; logique aussi ; dans ce cas, la vitesse devient très faible pour s'annuler à t=tm. (dv/dt) est très proche de (-g) : l'influence des frottements sur l'accélération devient négligeable.
Si tu as le temps, tu peux ensuite étudier la descente. Sans changer de repère, tu as intérêt à faire un décalage de l'origine des dates en posant t'=0 au passage au sommet. Ainsi : vo=0 ; zo=zm.
Au niveau de l'équation différentielle régissant la vitesse, cela conduit à remplacer g par (-g). Au lieu d'avoir une solution en arc-tangente, tu vas obtenir un argument de tangente hyperbolique.
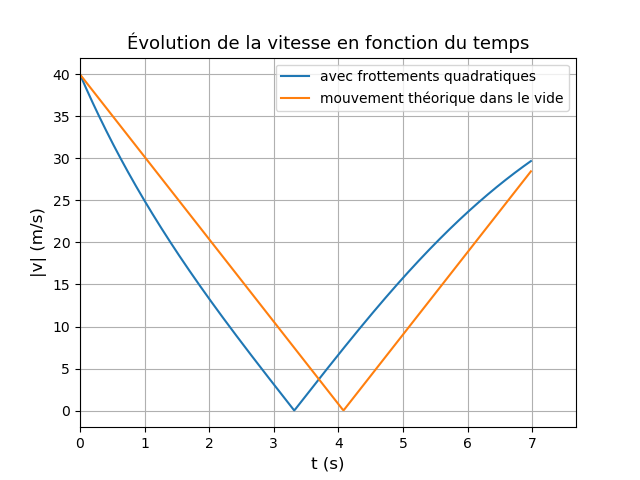
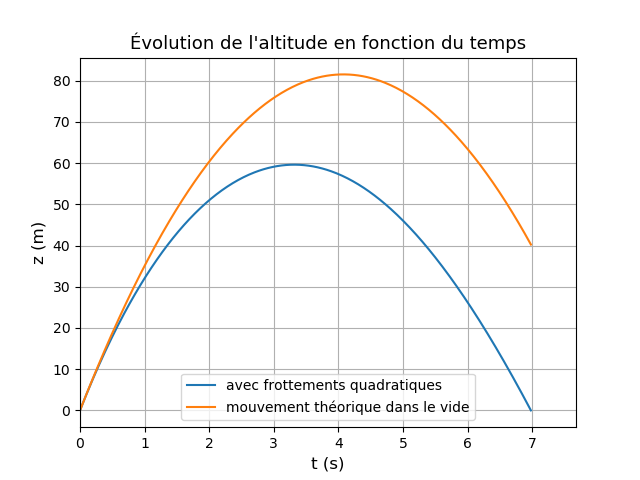
Pour te permettre de t'autocorriger, je te fournis une simulation avec les mêmes conditions initiales que précédemment. Cela conduit à une durée de descente :
ts=3,66s et à une vitesse d'arrivée au sol vs=29,7m/s (bien inférieure bien sûr avec la vitesse de lancer : 40m/s)
salut Vanoise
merci pour vos explications
j'essayer d'étudier la descente :
on a
ce qui donne :
on pose
on obtient
et par suite
ce formule me semble incorrect car on a à t =0
donne
je refaire le calcul plusieurs fois j'arrive pas à détecter l'erreur
Ce que tu as fait est globalement correct. Tu pourrais remarquer :
ce qui permettrait d'obtenir directement v en fonction de .
Logique : l'axe étant orienté vers le haut, la vitesse est constamment négative. De plus, cette limite s'obtient sans calcul à partir de la relation fondamentale de la dynamique. Au fur et à mesure de la descente, la vitesse augmente en norme, la force de frottement augmente, la vitesse tend vers une limite où la force de frottement compense exactement le poids : avec v<0.
J'ai repris tes calculs d'un peu plus près. Tu as sans doute commis une erreur de signe au niveau du logarithme en passant aux exponentielles. J'obtiens de mon côté :
On obtient bien ainsi :
v=0 pour t=0 et
Bonsoir Vanoise
Merci pour l'explication et la correction
donc on a :
or
on pose:
on obtient :
temps de descente (pour arriver au sol)
donne
ce qui donne :
multipliant par
posons et
car
implique
ou
je sais pas quel solution choisi
mais je suppose que le 1ère solution
donc :
D'accord avec ton équation horaire (oubli de « t » dans la dernière expression du cosh) :
Pour obtenir ts : date d'arrivée au sol, il n'est pas nécessaire de faire un changement de variable : y ? Tout simplement, en utilisant l'expression de zm obtenue en étudiant la montée :


