Bonjour, je suis en train d'essayer de coder mon propre, et modeste, moteur physique pour un jeu video. Pour l'instant j'ai juste implémenté la gravité à l'aide de la seconde loi de Newton, maintenant j'essaye de simuler le rebond.

Dans mon simulateur, j'ai une balle à laquelle je donne une position initiale, une vitesse initiale, une masse, un rayon, une élasticité ainsi que le milieu dans lequel elle trouve. Son élasticité, qui est une valeur comprise entre 0 et 1, va influer sur l'amplitude des rebonds : plus c'est proche de 1, plus les rebonds vont être importants.
Ce que je fais concrètement pour l'instant, c'est que lorsque je détecte une collision avec le sol, je réinitialise les conditions initiales comme suit :
- pos0 = position actuelle
- speed0.x = vitesse en x actuelle
- speed0.y = -(vitesse en y actuelle) * élasticité
- t0 = 0

C'est la vitesse initiale ici qui me permet de déclencher le rebond. Alors ça marche très bien en y, seul problème pour l'instant, comme je n'ai que le poids qui s'applique, me balle ne s'arrête jamais en x !
Il faut encore implémenter les frottements du sol (pour l'instant je néglige ceux de l'air). C'est là que je commence à sécher un peu.

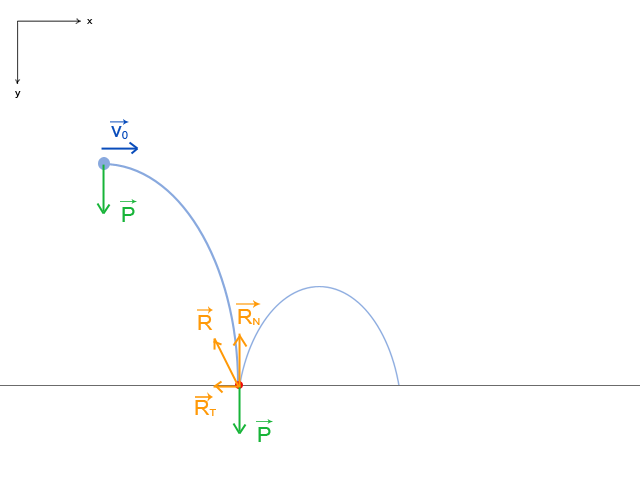
J'ai joint un petit schéma. Déjà j'aimerais savoir si j'ai bien représenté la Réaction ? Et ensuite est-ce bien cela qui va permettre de décroitre progressivement Vx ? Comme c'est une force ponctuelle ça me perturbe un peu... Aussi comment calculer le vecteur R ? Rn est-il toujours égal à P ?
Tout ce que je sais c'est que Rt = k*Rn, avec k dépendant de la nature des matériaux.

Enfin voila, si vous avez des indications/conseils à me donner pour terminer cette histoire de rebonds, je suis preneuse ^^

PS : Mes connaissances en mécanique se limite essentiellement à la Terminale S ^^"