Inscription / Connexion Nouveau Sujet
moteur asynchrone - bilan puissance
Bonjour
Je dois déterminer les grandeurs électriques suivantes de la machine asynchrone (voir fichier joint de l'enoncé):
Avec Is (courant statorique) = 0,35 A
Ir (courant rotorique) = 0,24 A
g (glissement) = 0,05
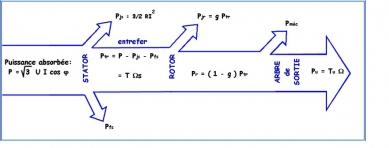
1- Calculer la puissance mecanique du moteur Pmec
Pmec = Tu x omega (n)
Tu (couple transmis au rotor) = (3 x R'r x I'r^2 ) / (g x omega n)
Tu = 0,496 N/M
Pmec = Tu x omega n
omega n = 2*pi x 950 / 60 = 99,4 rad/s
Pmec = Tu x omega n
Pmec = 0,498 x 99,4 = 49, 4 W
2- les pertes joules au stator et au rotor
Pjs = (3/2) * R*Is^2
Pjs = (3/2) * 30 * (0,35)^2
Pjs = 5,51 W
omega ns = 2*pi x 1000 / 60 = 104,71 rad/s
puissance transmise au rotor(Ptr) = T * omega ns
=51.93
Pjr = g * Ptr = 2,59
somme total pertes= 2,59 + 5,51 = 8,1 W
3- le rendement
rendement = Pmec / (Pmec +Pjs)
=49,4/ (49,4+5,51) = 0,899
Je ne suis pas sur du tout de mes calculs, si quelqu'un à une idée je suis preneur
** image supprimée => un énoncé doit être recopié **
Bonjour
Je t'ai déjà parlé de l'unité de moment de couple et tu commets ici exactement la même erreur. Toute application numérique non accompagnée de son unité correcte si celle-ci existe est considérée comme fausse un jour de concours ou d'examen.
Le reste semble logique mais sans énoncé complet...
Ci joint l'énoncé complet avec les questions ci dessous ainsi que les calculs:
1) Calcul du glissement g:
p = 3 paires de poles
ns = f /p = 50 / 3 = 16,66 tr/s soit 1000 tr/min
g = (ns - n) / ns
g= (1000 - 950) / 1000 = 0,05
2) Calcul du courant rotorique Ir:
O's= Xh / (Rs + XOs + Xh) = 824 / (30+30+824) = 0,932 ohm
Xcc = XOs + XO'r = 30 + 28 = 58 ohm
Ir = O's * Us / (racine(R's + R'r /g)^2 + Xcc^2)) = 0,24 A
3) Calcul du courant statorique Is:
Is = racine ((R'r/g)^2 + (X'Or + Xh)^2)) / Xh *Ir
Is = 0,35 A
4) Calcul de la puissance mécanique:
Pmec = Tu x omega (n)
Tu (couple transmis au rotor) = (3 x R'r x I'r^2 ) / (g x omega n)
Tu = 0,496 N.M
Pmec = Tu x omega n
omega n = 2*pi x 950 / 60 = 99,4 rad/s
Pmec = Tu x omega n
Pmec = 0,498 x 99,4 = 49, 4 W
5) Pertes joule:
Pjs = (3/2) * R*Is^2
Pjs = (3/2) * 30 * (0,35)^2
Pjs = 5,51 W
omega ns = 2*pi x 1000 / 60 = 104,71 rad/s
puissance transmise au rotor(Ptr) = T * omega ns
=51.93
Pjr = g * Ptr = 2,59
somme total pertes= 2,59 + 5,51 = 8,1 W
6) Rendement:
rendement = Pmec / (Pmec +Pjs)
=49,4/ (49,4+5,51) = 0,899
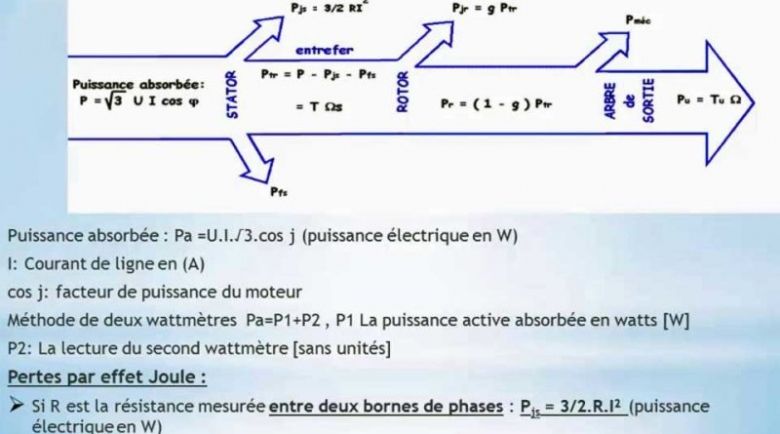
J'ai joué également le schéma du bilan des puissances de la machine asynchrone (j'ai un doute sur la calcul du couple utile (question 4), j'hesite encore a utilisé "omega s" (qui correspond à 1000 tr/min) et omega n (950 tr/min)
** image supprimée **
Les valeurs des résistances et des intensité permettent la déterminations des différentes pertes cuivre. Sans connaître la puissance électrique reçue par le moteur, difficile de déterminer la puissance mécanique.
La puissance électrique reçu par le moteur est la "puissance absorbée" défini par la relation Pa = U*I*racine(3)*cos phi
Le soucis est que nous connaissons pas le facteur de puissance cos phi.
Par contre, le courant de ligne I est égale au courant statorique Is (égale à 0.35 A)
Bonjour,
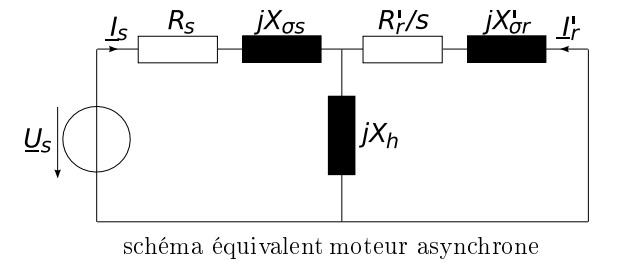
Voici l'enoncé complet (avec le schéma équivalent) avec les réponses,
les réponses aux question 1,5,6 et 7 demandent confirmation
Un moteur asynchrone couplé en étoile a les caractéristiques suivantes :
Nombre de pôles : 2p = 6
Tension nominale de phase : Us = 230V
Fréquence : f =50 hz
Vitesse nominale : 950 tr/min
Résistance statorique : Rs = 30 ohm
Résistance rotorique rapportée au stator : R'r = 43 ohm
Réactance de fuites statorique : Xos = 30 ohm
Réactance de fuites rotorique rapportée au stator : X'or = 28 ohm
Réactance de la branche magnétisante : Xh = 824 ohm
On néglige les pertes fer de la machine.
Calculer les grandeurs suivantes:
1) Determiner La résistance Re et la réactance Xe de l'équivalent de Thévenin sous forme complexe a+ j*b arrondi à une décimale.
Z = j*Xh / (Rs+ j*Xos + j*Xh) = 824j / (30+ 30j + 824j)
Z = 0,96 + 0,036j
2) Glissement g
p = 3 paires de poles
ns = f /p = 50 / 3 = 16,66 tr/s soit 1000 tr/min
g = (ns - n) / ns
g= (1000 - 950) / 1000 = 0,05
3) Valeur efficace du courant rotorique Ir
O's= Xh / (Rs + XOs + Xh) = 824 / (30+30+824) = 0,932 ohm
Xcc = XOs + XO'r = 30 + 28 = 58 ohm
Ir = O's * Us / (racine(R's + R'r /g)^2 + Xcc^2)) = 0,24 A
4) Valeur efficace du courant statorique Is
Is = racine ((R'r/g)^2 + (X'Or + Xh)^2)) / Xh *Ir
Is = 0,35 A
5) Puissance Mecanique du moteur
Pmec = Tu x omega (n) -> je suis parti de cette relation là car nous ne connaissons pas le courant de ligne I et le facteur de puissance cos phi.
Tu (couple transmis au rotor) = (3 x R'r x I'r^2 ) / (g x omega n)
Tu = 0,496 N.M
Pmec = Tu x omega n
omega n = 2*pi x 950 / 60 = 99,4 rad/s
Pmec = Tu x omega n
Pmec = 0,498 x 99,4 = 49, 4 W
6) Sommes des pertes joule au stator et au rotor
Pjs = (3/2) * R*Is^2
Pjs = (3/2) * 30 * (0,35)^2
Pjs = 5,51 W
omega ns = 2*pi x 1000 / 60 = 104,71 rad/s
puissance transmise au rotor(Ptr) = T * omega ns
=51.93
Pjr = g * Ptr = 2,59
somme total pertes= 2,59 + 5,51 = 8,1 W
7) Rendement
rendement = Pmec / (Pmec +Pjs)
=49,4/ (49,4+5,51) = 0,899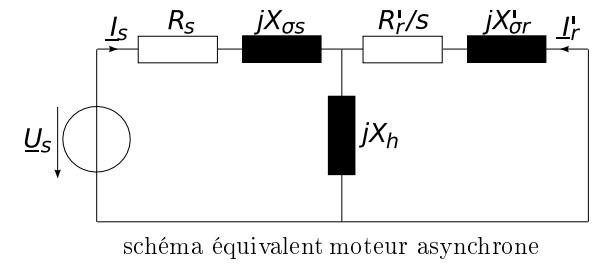
***Edit gbm : merci pour la recopie  ***
***
Tu peux déduire le facteur de puissance manquant de l'expression de l'impédance complexe.
Ayant ainsi la puissance électrique reçue, tu soustrais les pertes cuivre (pertes fer négligées) et il te reste la puissance mécanique.
Rappel de l'énoncé
Un moteur asynchrone couplé en étoile a les caractéristiques suivantes :
Nombre de pôles : 2p = 6
Tension nominale de phase : Us = 230V
Fréquence : f =50 hz
Vitesse nominale : 950 tr/min
Résistance statorique : Rs = 30 ohm
Résistance rotorique rapportée au stator : R'r = 43 ohm
Réactance de fuites statorique : Xos = 30 ohm
Réactance de fuites rotorique rapportée au stator : X'or = 28 ohm
Réactance de la branche magnétisante : Xh = 824 ohm
On néglige les pertes fer de la machine.
Calculer les grandeurs suivantes:
1- Calculer la puissance mecanique du moteur Pmec:
Etape 1: Calcul de l'impedance totale (voir schéma équivalent en pièce jointe):
Zt = (Xh * (R'r + Rs + XoS + X'os)) / (Xh + R'r + Rs + Xos + X'os)
Zt = 113 ohm
Etape 2: Calcul du courant de ligne I:
I = U/Z = 230 / 113 = 2,03 A
Etape 3: Calcul de cos phi:
tan phi = Xe / Re
Xe = (Xh * (X'os +Xor )) / ( Xh + X'os + Xor) = 54, 18 ohm
Re = Rs + R'e = 30 + 43 = 73 ohm
tan phi = 0,739 -> phi = 36,46 soit cos phi = 0,804
Etape 4: Calcul de Pa
Pa = UI racine(3) cos phi
Pa = 230 * 2,03 *racine(3) * 0,804 = 650,19 W
Etape 5: Calcul des pertes joules au stator:
Pjs = (3/2) * Rs * Is^2
Pjs = (3/2) * 30 * (0,35^2) = 5,51 W
Etape 6 : Calcul de la puissance transmise au rotor (pertes fer negligées):
Ptr = Pa - Pjs
Ptr = 650,19 - 5,51 = 644,67 W
Ainsi la puissance mécanique s'effectue par la relation suivante:
Pm = Ptr (1 - g) = 644,67 * 0,95 = 612,43 W
2- les pertes joules au stator et au rotor:
Pjs = (3/2) * R*Is^2
Pjs = (3/2) * 30 * (0,35)^2
Pjs = 5,51 W
Pjr = g * Ptr = 0,05 * 644,67 = 32,23 W
somme total pertes= 32,23 + 5,51 = 37,74 W
3- le rendement
rendement = (Pa - Pjs - Pjr) / (Pa)
=612,45/ 650,19 = 0,94
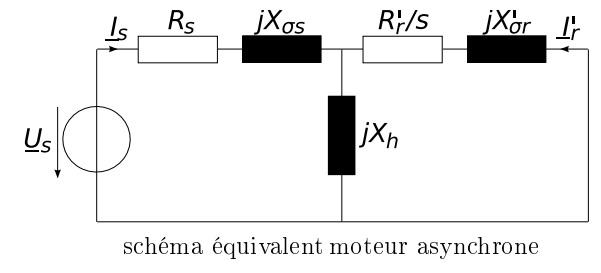
Ta façon de calculer séparément partie réelle et partie imaginaire de Z est originale mais fausse. En se fiant au circuit équivalent fourni, il faut considérer l'impédance équivalente du moteur comme l'association en série de deux impédances complexes :
L'impédance complexe Z1=Rs+jX s
s
L'impédance complexe Ze équivalente à l'association en parallèle de deux impédances complexes :
Z2=jXh
Z3=R'r/g+jX' r
r
Ok voici les calculs avec les modifications concernant le calcul de l'impedance,
RAPPEL du sujet et des questions:
Un moteur asynchrone couplé en étoile a les caractéristiques suivantes :
Nombre de pôles : 2p = 6
Tension nominale de phase : Us = 230V
Fréquence : f =50 hz
Vitesse nominale : 950 tr/min
Résistance statorique : Rs = 30 ohm
Résistance rotorique rapportée au stator : R'r = 43 ohm
Réactance de fuites statorique : Xos = 30 ohm
Réactance de fuites rotorique rapportée au stator : X'or = 28 ohm
Réactance de la branche magnétisante : Xh = 824 ohm
On néglige les pertes fer de la machine.
Calculer les grandeurs suivantes:
1- Calculer la puissance mecanique du moteur Pmec:
Etape 1: Calcul de l'impedance totale Ze (voir schéma équivalent en pièce jointe):
Z1 = Rs + j Xos
Z2 = jXh
Z3 = R'r/g + jX'or
Z2 et Z3 sont en paralleles
Ze23 = (Z2 * Z3) / (Z2 + Z3)
= 614 , 36 ohm
Ze = Ze23 + Z1 = 656, 78 ohm
Etape 2: Calcul du courant de ligne I:
I = U/Z = 230 / 656,78 = 0,35 A
Etape 3: Calcul de cos phi:
tan phi = Xe / Re
Xe23 = (Xh * X'os) / (Xh + X'os) = 27 ohm
Xe = X1 + X23 = 57 ohm
Re = Rs + R'e = 57 ohm
tan phi = Xe/Re = 0,78 -> phi = 37,98 soit cos phi = 0,788
Etape 4: Calcul de Pa
Pa = UI racine(3) cos phi
Pa = 230 * 0,35 *racine(3) * 0,788 = 109,87 W
Etape 5: Calcul des pertes joules au stator:
Pjs = (3/2) * Rs * Is^2
Pjs = (3/2) * 30 * (0,35^2) = 5,51 W
Etape 6 : Calcul de la puissance transmise au rotor (pertes fer negligées):
Ptr = Pa - Pjs
Ptr = 109,87 - 5,51 = 104,36 W
Ainsi la puissance mécanique s'effectue par la relation suivante:
Pm = Ptr (1 - g) = 104,36 * 0,95 = 99,14 W
2- les pertes joules au stator et au rotor:
Pjs = (3/2) * R*Is^2
Pjs = (3/2) * 30 * (0,35)^2
Pjs = 5,51 W
Pjr = g * Ptr = 0,05 * 109,87 = 5,49 W
somme total pertes= 5,49 + 5,51 = 10 W
3- le rendement
rendement = (Pa - Pjs - Pjr) / (Pa)
=98,87/ 109,87 = 0,89
Il faut calculer la somme des impédances complexes Z1 et Ze23. Comme l'énoncé le précise, tu obtiens alors l'impédance équivalente sous la forme Z=a+jb et ce n'est qu'à ce stade que tu détermines le module et l'argument.
Ze23 = jXh * (R'r/s + jX'or) / jXh +R'r/s + JX'or)
= (43000j - 1400j^2) / (78j + 860) = 551 j - 1,62
Ze = Z1 + Ze23
Ze = 28,4 + 581j
Ze= racine (Re^2 + Xe^2) = 581, 69 ohm
Je t'ai peut-être induit en erreur : la détermination de la résistance rotorique rapportée au stator : R'r/s fait intervenir la valeur de g mais il semble bien que la valeur fournie tienne déjà compte de g et qu'il convient de poser : R'r/s=43 . Il n'y a pas lieu de diviser cette valeur par g. Quoi qu'il en soit, je pense que tu as tout de même un problème de manipulation des nombres complexes : que je pose R'r/s=43
. Il n'y a pas lieu de diviser cette valeur par g. Quoi qu'il en soit, je pense que tu as tout de même un problème de manipulation des nombres complexes : que je pose R'r/s=43 ou 860
ou 860 , je n'obtiens pas les mêmes valeurs que toi.
, je n'obtiens pas les mêmes valeurs que toi.
D'accord avec ton expression littérale de Ze23 mais pas d'accord avec l'application numérique. J'obtiens :
Ci dessous les grandeurs calculés en tenant compte de la modification du calcul de l'impedance Ze (voir énoncé dans les messages précédent)
1- Calculer la puissance mecanique du moteur Pmec:
Etape 1: Calcul de l'impedance totale Ze (voir schéma équivalent en pièce jointe):
Z1 = Rs + j Xos
Z2 = jXh
Z3 = R'r/g + jX'or
Ze23 = jXh * (R'r + j Xor) / (jXh + R's + jX'or)
= 824j * (43+28j) / (43 + 852j)
= 40,1 + 29,1j
Ze= 40,1 + 29,1j + 30 + 30j
Ze = 70,1 + 59,1j
Ze= racine(Re^2 + Xe^2)
Ze= racine (70,1^2 + 59,1^2)= 91,68 ohm
Etape 2: Calcul du courant de ligne I:
I = U/Z = 230 / 91,68 = 2,51 A
Etape 3: Calcul de cos phi:
tan phi = Xe / Re
tan phi = 59,1/70,1 = 0,843 -> phi = 40,1 soit cos phi = 0,764
Etape 4: Calcul de Pa
Pa = UI racine(3) cos phi
Pa = 230 * 2,51 *racine(3) * 0,764 = 763,93 W
Etape 5: Calcul des pertes joules au stator:
Pjs = (3/2) * Rs * Is^2
Pjs = (3/2) * 30 * (0,35^2) = 5,51 W
Etape 6 : Calcul de la puissance transmise au rotor (pertes fer negligées):
Ptr = Pa - Pjs
Ptr = 763,93 - 5,51 = 758,42 W
Ainsi la puissance mécanique s'effectue par la relation suivante:
Pm = Ptr (1 - g) = 758,42 * 0,95 = 720,5 W
2- les pertes joules au stator et au rotor:
Pjs = (3/2) * R*Is^2
Pjs = (3/2) * 30 * (0,35)^2
Pjs = 5,51 W
Pjr = g * Ptr = 0,05 * 758,42 = 37,92 W
somme total pertes= 37,92 + 5,51 = 43,43 W
3- le rendement
rendement = (Pa - Pjs - Pjr) / (Pa)
=720,5/ 763,93 = 0,94
D'accord avec ce que tu as fait. J'ai juste un doute à propos des pertes par effet Joule . Faut-il les calculer à partir des valeurs de Ir et Is fournies dans ton premier message ou faut-il déduire ces deux intensités du modèle équivalent ? Cela ne donne pas la même chose.
Tu veux dire que pour les pertes joules, il faut utiliser I qui est calculé en faisant le rapport de U sur Z au lieu de Is pour les pertes joules au stator et Ir pour celles liées au rotor?
En regardant le document mis en attachement (bilan puissance MAS), je pense qu'il faut utiliser le courant de ligne I. Je vais refaire les calculs
Nous ne nous sommes pas compris. Dans ton tout premier message, tu écris :
Is=0,35A
Ir=0,24A
Ces valeurs sont fournies par l'énoncé ou c'est toi qui les a calculées ? On n'obtient pas ces valeurs-là en raisonnant sur le circuit équivalent.
Tu es bien sûr de ces valeurs ? Comment les as-tu calculées ? Elles ne correspondent pas à celles déduites du schéma équivalent.
Pour calculer Ir et Is, on calcule les grandeurs suivantes (voir ci joint schéma equivalent modele de thevenin):
s (glissement) = 0,05 (valeur precedemment calculer)
1) Calcul de Ir:
Os = Xh / (Rs +Xos +Xh) = 824 / (30+30+824) = 0,932
Xcc = X'os + X'or = 58 ohm
Ir = (Os * Us) / racine((R's + R'r/s)^2 + Xcc^2)) = 214,36 / 889,85
Ir = 0,24 A
2) Calcul de Is:
Is = racine((R'r/s)^2 + (X'or + Xcc)^2) / Xh *Ir
Is = (1210,58 / 824) * 0,24
Is = 0,35 A
Par contre, concernant le calcul de l'impedance complexe Ze=Re+Xe, je pense qu'il faut partir du modele equivalent de thevenin:
R's + jX'os = Os *(Rs + jXos)
27,96 + 30j = 0,932 * (30 + 30j)
Ze = 27,96 + 30j
Je ne suis pas sur de mon calcul concernant l'impedance complexe Ze
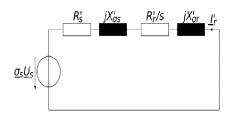
R's + jX'os = Os *(Rs + jXos)
27,96 + 30j = 0,932 * (30 + 30j)
Ze = 27,96 + 30j
Étourderie de calcul, il me semble.
Ok, j'ai refait du coup les calculs suivants:
1- Calculer la puissance mecanique du moteur Pmec:
avec l'impedance complexe Ze = 27,9 + 30j
Ze= racine(Re^2 + Xe^2)
Ze= racine (27,9^2 + 30^2)= 40,96 ohm
Etape 2: Calcul du courant de ligne I:
I = U/Z = 230 / 40,96 = 5,61 A
Etape 3: Calcul de cos phi:
tan phi = Xe / Re
tan phi = 30/27,9 = 1,07 -> phi = 47 soit cos phi = 0,681
Etape 4: Calcul de Pa
Pa = UI racine(3) cos phi
Pa = 230 * 5,61 *racine(3) * 0,681 = 1521,97 W
Etape 5: Calcul des pertes joules au stator:
Pjs = (3/2) * Rs * Is^2
Pjs = (3/2) * 30 * (0,35^2) = 5,51 W
Etape 6 : Calcul de la puissance transmise au rotor (pertes fer negligées):
Ptr = Pa - Pjs
Ptr = 1521,9 - 5,51 = 1516,46 W
Ainsi la puissance mécanique s'effectue par la relation suivante:
Pm = Ptr (1 - g) = 1516,46 * 0,95 = 1440,63 W
2- les pertes joules au stator et au rotor:
Pjs = (3/2) * R*Is^2
Pjs = (3/2) * 30 * (0,35)^2
Pjs = 5,51 W
Pjr = g * Ptr = 0,05 * 1516,46 = 75,82 W
somme total pertes= 75,82 + 5,51 = 81,33 W
3- le rendement
rendement = (Pa - Pjs - Pjr) / (Pa)
=1440,64/ 1521,97 = 0,94
par contre je ne suis pas sur de mon raisonnement pour le calcul de I (calcul de I en fonction de l'impedance totale Ze et Us), j'ai hésité à utilisé le courant Is (courant statorique) pour les calculs des puissances
Selon moi, l'alimentation électrique du moteur fournit du courant aux bobines du stator. Si le rotor est parcouru par un courant, c'est grâce au phénomène d'induction qui apparaît lorsque le glissement n'est pas nul.
voici les nouveaux calculs:
Ok, j'ai refait du coup les calculs suivants:
1- Calculer la puissance mecanique du moteur Pmec:
avec l'impedance complexe Ze = 27,9 + 30j
Ze= racine(Re^2 + Xe^2)
Ze= racine (27,9^2 + 30^2)= 40,96 ohm
Etape 2: Calcul de cos phi:
tan phi = Xe / Re
tan phi = 30/27,9 = 1,07 -> phi = 47 soit cos phi = 0,681
Etape 3: Calcul de Pa
I = Is = 0,35 A
Pa = UI racine(3) cos phi
Pa = 230 * 0,35 *racine(3) * 0,681 = 94,95 W
Etape 5: Calcul des pertes joules au stator:
Pjs = (3/2) * Rs * Is^2
Pjs = (3/2) * 30 * (0,35^2) = 5,51 W
Etape 6 : Calcul de la puissance transmise au rotor (pertes fer negligées):
Ptr = Pa - Pjs
Ptr = 94,95 - 5,51 = 89,44 W
Ainsi la puissance mécanique s'effectue par la relation suivante:
Pm = Ptr (1 - g) = 89,44 * 0,95 = 84,96 W
2- les pertes joules au stator et au rotor:
Pjs = (3/2) * R*Is^2
Pjs = (3/2) * 30 * (0,35)^2
Pjs = 5,51 W
Pjr = g * Ptr = 0,05 * 89,44 = 4,47 W
somme total pertes= 4,47 + 5,51 = 9,9 W
3- le rendement
rendement = (Pa - Pjs - Pjr) / (Pa)
=84,97/ 94,95 = 0,89