Inscription / Connexion Nouveau Sujet
Montagnes russes
Bonjour, en vu de notre TPE nous avons à partir de plusieurs exercices créée une "démonstration", et nous voudrions savoir si c'est bon :
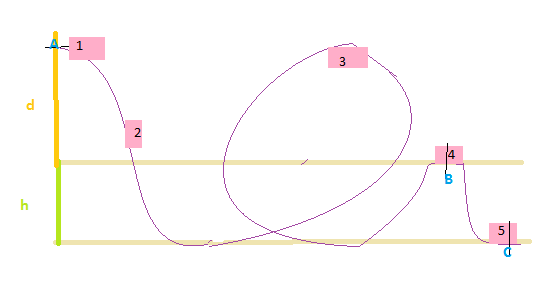
On se base sur ce circuit ( voir image ) :
Le système étudié est le chariot dans un référentiel galiléen. Dans un premier temps, les frottements sont négligeables. Au point A la vitesse est nulle.
1) Les énergies :
A la position 1, le chariot a de l'énergie potentielle car il a une altitude mais pas de vitesse.
A la position 2,3 et 5 le chariot a de l'énergie potentielle et cinétique car le wagon a de l'altitude et de la vitesse.
A la position 6, le chariot a de l'énergie cinétique car il a de la vitesse mais pas d'altitude
A la position 1, le chariot a de l'énergie potentielle puis son altitude diminue en position 2 donc son énergie potentielle aussi. Durant sa descente il gagne de l'énergie cinétique : l'énergie potentielle s'est transformé en énergie cinétique. En gagnant de l'altitude en position 3, le chariot transforme une partie de son énergie cinétique en énergie potentielle. En position 4, le chariot perd toute son altitude et ainsi son énergie potentielle, elle est devenue de l'énergie cinétique. Ensuite le chariot va en position 5, il regagne de l'altitude et donc de l'énergie potentielle puis à la position 6 il n'a plus d'altitude donc toute son énergie potentielle s'est transformé en énergie cinétique. L'énergie mécanique correspond à la somme des valeurs de l'énergie potentielle et cinétique, sa valeur reste constante tout le long du trajet.
2) Les vitesses : ( la vitesse au point A est nulle )
Energie potentielle : mgz et Energie cinétique : 1/2mv2
Pour le point A : zA= d+h
EppA= mg*(d+h)
Pour le point B : zB=h
L'énergie mécanique se conserve donc EmA=EmB
On peut conclure que EppA+EcA=EppB+EcB
EmA= 1/2mva2 + mg(d+h) on considère vA=0
Donc EmA) = mg(d+h)
EmB+EmA = 0 + mgd + mgh= 1/2mvB2 + mgh
Après simplification on obtient :
gd = 1/2vB2
Donc vB + 2gd
2gd
→ La formule de la vitesse vB s'applique aux positions 2,3 et 5 car ils ont tous trois les même énergies mais les valeurs ne sont pas les même.
Calcul de la vitesse vC: Ema = Emc
Ema = (1/2)Mva² + Mg (d+h) → Ema = Mg (d+h)
Emc = (1/2)Mva² + Mg (d+h) → Emc = (½) Mvc²
Mg (d+t) = (½) Mvc²
 2*(g(d+h)) = vC
2*(g(d+h)) = vC
VC= 2gd+2gh
2gd+2gh
→ La formule de la vitesse vC s'applique également aux positions 4 et 6 mais les valeurs ne sont pas les mêmes.
Voilà c'est qu'une esquisse, on sait pas si tous nos calculs litteraux sont bon ...
Merci !
Edit Coll : forum modifié
Bonjour,
1) Ok. Si les frottements sont négligeables (ou négligés), on peut écrire: Em=Ec+Ep=cste ce qui veut dire, comme tu l'as bien dit, qu'il y a en permanence conversion de l'énergie cinétique en énergie potentielle et inversement.
2) Je n'aime pas trop cette écriture
EmB+EmA = 0 + mgd + mgh= 1/2mvB2 + mgh
Je l'aurai noté de cette façon (bien que ça revient au même mais ton équation telle qu'elle est écrit n'est pas très claire):
Em=Ec+Ep=cste
Donc: EmA=EmB <=> EcA+EpA=EcB+EpB
<=> (1/2).m.vA²+mg.zA=(1/2)m.vB²+mg.zB
Or vA=0m/s donc on a:
<=> mg.zA=(1/2)m.vB²+mg.zB
On isole VB²:
vB²=2g(zA-zB)
On remplace zA et zB par leurs expressions:
vB²=2g(d+h-h)
Donc, on a:
Pour une petite précision et un oubli fréquent de beaucoup d'élèves, mathématiquement lorsque l'on prend la racine carré de vB², on obtient:
Ce qui veut dire que:
Mais d'un point de vue physique, une vitesse négative n'a pas de sens (en tout cas lorsqu'on parle de scalaire). Si tu avais vu ça et que c'est pour cette raison que tu as mis un + devant ton résultat, c'est bien mais un petit rappel ne fait jamais de mal.
Sinon pour ta conclusion à cette vitesse vB, oui c'est correcte puisque l'énergie se conserve, tu as donc la relation littérale et lorsque tu voudras trouver les vitesses aux différents points, il suffit de remplacer d par la hauteur entre l'altitude h et le point que tu as choisi.
Bon j'avoue que sans schéma, j'ai un peu de mal à visualiser où sont positionner tes points A,B et C ( de ce que j'ai cru comprendre, le point C se situe à la distance d=-h d'où h+d=h-h=0) mais d'un point de vue calcul c'est correct.