Inscription / Connexion Nouveau Sujet
Moments et réactions de support
Bonsoir.
Je suis en train d'étudier un exercice, dont voici le sujet :
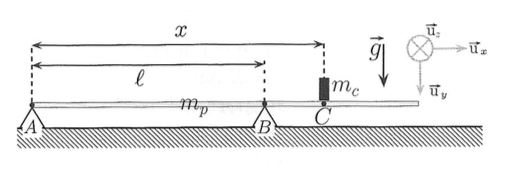
Une poutre de masse mP=60 kg et de longueur L=5 m repose sur deux supports A et B séparés d'une distance l=3 m.
Un individu de masse mC=80 kg se déplace le long de la poutre en partant de son extrémité A et il est repéré à chaque instant par le point C.
- Tous les contacts sont supposés ponctuels.
- On note f le coefficient de frottement entre la poutre et le contact en B et JB=1/9*mP*L2 son moment d'inertie par rapport à l'axe (B,).
- La poutre est homogène et son centre d'inertie noté G est situé à la distance L/2 de A.
Questions :
a) Déterminer la réaction du support au point A en fonction de x et des paramètres du problème.
b) Déterminer numériquement la distance maximale xmax à laquelle peut s'éloigner l'individu tout en conservant la poutre parfaitement horizontale.
c) On suppose que l'individu se place à la distance xmax+ (
( >0), la poutre bascule autour du point B sans vitesse initiale et sans glissement.
>0), la poutre bascule autour du point B sans vitesse initiale et sans glissement.
Déterminer les composantes normale et tangentielle de la réaction en B.
À partir de quel angle le glissement commence-t-il ?
Mes idées :
a) J'ai essayé quelque chose, je ne sais pas si c'est correct.
Théorème du moment cinétique :
(j'exprime les moments des formes par rapport au point G à l'équilibre)
Donc : puis en calculant les produits vectoriels et en projetant sur z, j'ai :
et avec
à l'équilibre, j'ai finalement :
b) Je pense exprimer le moment du poids de l'individu par rapport au point B où a lieu la liaison pivot et dire que, pour que la poutre reste horizontale, mais je trouve bizarrement que x=l ce dont je doute fortement.
Dois-je prendre en compte les autres forces ? Je pense mais je n'en étais pas sûre.
c) Je n'ai pas trop d'idées : un théorème du moment cinétique ?
Merci d'avance pour vos réponses.
Bonsoir
Je crois que tu as commis une erreur de calcul : la distance GB n'est pas égale à L/2.
Pour les questions a et b, il me semble plus simple d'appliquer le théorème des moments statiques directement au point B ; ainsi RB n'intervient pas et on obtient directement RA sans utiliser le théorème de la résultante statique.
Pour la question c) il faut effectivement appliquer le théorème du moment dynamique par rapport à l'axe de la liaison pivot ainsi que le théorème du centre d'inertie.
Je te laisse rectifier par toi-même.
Bonsoir.
Donc je peux me passer de G et faire tous les calculs en B ?
Et oui, je me suis effectivement trompée sur GB. Je vais revoir cela.
Que puis-je faire pour la question b) ? Mon résultat semble bizarre.
Ah oui, je comprends mieux maintenant l'intérêt de la question a par rapport à la b !
En revanche je bloque pour la c : je ne sais pas quoi poser en équation.
Pour c) l'ensemble {poutre - individu} peut être considéré comme un solide en rotation autour d'un axe fixe (B,z) passant par B et perpendiculaire au plan de figure. Tu peux appliquer le théorème du moment cinétique à ce solide. Compte tenu de la "largeur" de l'individu par rapport à la longueur de la poutre, tu peux calculer le moment d'inertie de l'individu comme s'il s'agissait d'une masse ponctuelle . Ayant ainsi l'accélération angulaire, tu pourra calculer l'accélération de G puis la RFD te donnera les composantes normale et tangentielle de la réaction en B.
Loi de Coulomb sur les frottements solides pour finir...
Je te laisse réfléchir à tout cela et proposer une solution.
Au vu de tes indications, j'ai raisonné comme ça : j'ai considéré que l'individu avait fait tourné la poutre et que, dès lors, celle-ci faisait un angle  avec l'horizontale.
avec l'horizontale.
D'après le théorème du moment cinétique pour le solide en rotation, j'ai :
(JB+JH)=
Le problème, c'est que je ne sais pas quoi faire de la vitesse angulaire .
Choisit une base polaire. Ayant par le théorème du moment cinétique et
par la conservation de l'énergie mécanique, la connaissance de la distance BG va te permettre d'obtenir les composantes tangentielle et normale de l'accélération de G puisque G est en mouvement circulaire. Ensuite la RFD ...
Je ne sais pas si la notation  suppose
suppose  <<xmax...
<<xmax...
Je suis désolée mais j'ai vraiment du mal à visualiser tout ce qu'il faut faire.
Quel système à considérer ?
Le système poutre+personne.
Je vais d'ici demain te poster un schéma commentė et quelques aides supplementaires
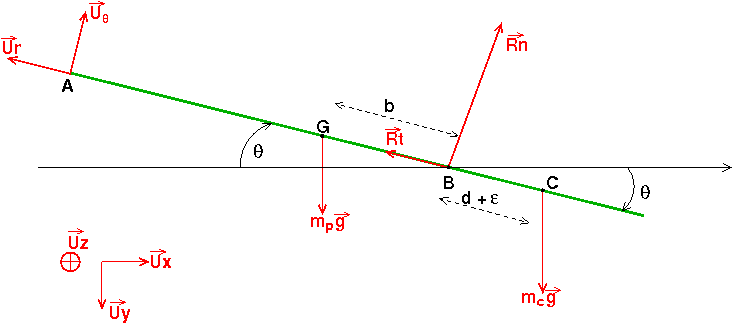
Le référentiel d'étude est la terre, considérée comme un référentiel galiléen. Pour simplifier un peu les notations, je pose : BG=b=l-L/2=0,5m et (xmax-l)=d. La position de C telle que x=xmax correspond à un équilibre de l'ensemble S:{poutre+individu} en absence de contact en A. En posant BC=d à l'équilibre, cela correspond à :
Lorsque , la poutre est en déséquilibre et tend à tourner dans le sens positif (sens horaire) autour de l'axe (B,z). En posant :
le théorème du moment cinétique appliqué à l'ensemble S , considéré comme un solide mobile autour de l'axe fixe (B,z) conduit à :
En supposant la liaison pivot idéale, on peut considérer que l'énergie mécanique se conserve entre l'instant où l'extrémité A décolle sans vitesse initiale et un instant quelconque correspondant à la figure.
G est en mouvement circulaire accéléré autour de l'axe (B,z), G décrit un cercle de rayon b et de centre B. Son accélération a pour expression :
La relation fondamentale de la dynamique appliqué au système S conduit à :
Cette résultante des actions extérieures pouvant s'écrire :
Je te laisse terminer les calculs et identifier...
Pour terminer : les lois de Coulomb sur les frottements entre solides imposent comme condition d'absence de glissement :
où est le coefficient de frottement statique.
Il se fait tard... Une erreur de calcul est évidemment possible mais tu as la méthode...
Mon approche aurait été celle-ci :
a)
Si x est tel que la poutre ne bascule pas :
RA + RB = g * (mp + mc)
MB = - RA*l + mp.g * (l - L/2) - mc * g * (x - l) = 0
RA = [mp.g * (l - L/2) - mc * g * (x - l)]/l
RA = [60*10 * (3 - 5/2) - 80 * 10 * (x - 3)]/3
RA = 900 - 800x/3
---
b)
Pour x, à la limite de basculement autour de B ...
RA = 0
900 - 800x/3 = 0
x = 3,375 m
---
c)
|RA| = 0
|RB| = g(mp + mc)
Rn = |RB| * cos(theta)
Rt = |RB| * sin(theta)
Or Rt max = f * Rn (avec f comme défini dans l'énoncé)
--> f * |RB| * cos(theta max) = |RB| * sin(theta max)
tg(theta max) = f
theta max = arctg(f)
Le glissement commence pour theta = arctg(f)
---
Rien relu. 
JP utilise une approche quasi statique du problème ; il raisonne comme si l'accélération angulaire et l'accélération de G étaient nulles avec 
 0...
0...
C'est une approche très simplifiée possible mais rien ne dit dans l'énoncé que  <<xmax et surtout : pourquoi le concepteur de ce problème s'est-il donné la peine de fournir le moment d'inertie JB si ce n'est pour demander une étude plus rigoureuse ?
<<xmax et surtout : pourquoi le concepteur de ce problème s'est-il donné la peine de fournir le moment d'inertie JB si ce n'est pour demander une étude plus rigoureuse ?
En reprenant mes équations et en posant :
 =0 ;
=0 ; ;
 =0 ;
=0 ; ,
tu vas retomber sur les résultats de JP. A toi de voir si c'est bien cette version très simplifiée qui t'est demandée.


