Inscription / Connexion Nouveau Sujet
Moment/Matrice d'Inertie d'un Solide
Bonjour,
Je bloque sur un exercice de concours en mécanique concernant le Moment/Matrice d'Inertie d'un Solide.
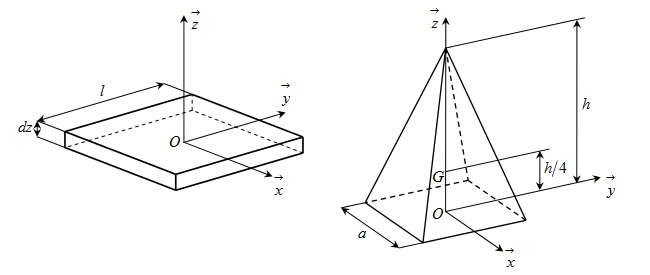
On considère tout d'abord une plaque carrée de côté l, d'épaisseur dz et de centre de masse O. Elle est constituée d'un matériau homogène de masse volumique ρ. L'axe Oz est perpendiculaire à la plaque. Les côtés de la plaque sont parallèles aux axes Ox et Oy.
Le référentiel ℜ est considéré comme galiléen. Il est rapporté au repère (O,x,y,z).
1.1 Déterminer le moment d'inertie dJ de la plaque par rapport à l'axe Oz.
dJ = r² dm
= (
x²+y²)² dm
= (x²+y²) dm
= (x²+y²) ρ*dV
= ρ(x²+y²) dx dy dz.
On s'intéresse maintenant à une pyramide droite (P), de base carrée de côté a et de hauteur h, constituée du même matériau que la plaque carrée.
O note M = 1/3 ρ a² h la masse de la pyramide droite (P) et OG = h/4 z le vecteur position du centre de
masse G de la pyramide (P).
1.2 La matrice d'inertie de la pyramide (P) dans le repère (G,x,y,z) est de la forme :
JX 0 0
0 JX 0
0 0 JZ
Justifier la forme de la matrice d'inertie de (P) dans le repère (G,x,y,z).
La pyramide possède une symétrie selon les plans (xOz) et (yOz) donc la matrice d'inertie et diagonale.
De plus, JX = JY car les axes x et y jouent le même rôle du point de vue géométrique et du point de vue de la répartition des masses.
1.3 A l'aide de la question 1.1, déterminer le moment d'inertie JZ de la pyramide (P) par rapport à l'axe Gz en fonction de M,a et h.
JZ = 1/3 ρ 
-a/2a/2 -a/2a/2 0h (x²+y²) dx dy dz
= M/6 a².
On donne le moment d'inertie JGxy = 3/80 M h² de la pyramide (P) par rapport au plan (G,x,y).
1.4 En déduire le moment d'inertie JX de la pyramide (P) par rapport à l'axe Gx.
Je ne vois pas comment en déduire car je ne vois pas ce que c'est que le moment d'inertie par rapport à un plan... Donc j'ai essayé de le calculer directement.
JX = 1/3 ρ -a/2a/2 -a/2a/2 0h (y²+z²) dx dy dz
= M/12 (a²+4h²).
La pyramide (P) tourne maintenant autour de l'axe Ox à la vitesse ω = ω x.
1.5 Exprimer dans la base liée à ℜ le moment cinétique LO(P/ℜ) de la pyramide (P) par rapport à ℜ au point O.
...
Merci d'avance.
Bonjour
dJ est le moment de la plaque d'épaisseur dz, tu dois exprimer dJ en fonction de x, y et dz après avoir intégré sur la surafce.
Après, pour la pyramide, tu pourras ainsi exprimer le moment élémentaire d'une épaisseur dz à la hauteur z (h dans ton dessin) sachant que les propriétés géométriques de la pyramide te donne x et y (longueur et largeur à la hauteur z) an fonction de z et de a (x = y = a pour z = 0)
T'ai je mis sur la voie?
Courage!
Il faut que je calcule la matrice d'inertie pour le point O puis que j'utilise le Théorème de Hyugens pour le point G.
Bonjour!
Ce que je voulais dire hier soir, c'est que dJ qui t'es demandé en 1.1) est le moment d'une plaque carrée de côté l et d'épaisseur dz
donc en coordonnées cartésiennes dans le repère Oxyz de la permière figure
dJ = 
dz.-l/2l/2-l/2l/2 (x2+y2) dxdy
Pour intégrer sur la surface de la plaque tu peux passer en coordonnées cylindriques où conserver les coordonnées cartésiennes.
Tu dois trouver en final qlq chose comme
dJ= 1/6..l4.dz
Ensuite pour la pyramide tu dois intégrer dJ sur l'ensemble de la hauteur h
Dans le repère Oxyz la coordonnée z d'une plaque d'épaisseur dz te permet de trouver l
l = a.(1 - z/h)
Dans le calcul que tu fais en 1.3 tu intégres systématiquement x et y entre -a/2 et a/2 alors que la plaque élémentaire a une longueur de côté fonction de z (cf. ci dessus).
Ai je été plus clair?
Re-,
Je viens de prendre connaissance du 1.4) (déduire Jx)
Tu as les égalités suivantes:
Jx = Jxz + Jxy (1)
Jy = Jyz + Jxy (2)
Avec, par symétrie
Jx = Jy
et par ailleurs
Jz = Jxz + Jyz (3)
Donc
2.Jx = Jz + Jxy
Tu as donc trouvé Jx, puisque Jz a été calculé précédemment et Jxy est donné par l'énnoncé
Si les égalités (1) (2) (3) ne sont pas familières, fais moi signe, nous prendrons le temps de les démontrer!
Courage!
Pour les égalités (1) (2) et (3) je les comprends, en fait c'est :
r² dm et r et simplement la distance entre un point du solide et le plan en question.
Sinon je crois que tu as oublié juste un 2 :
2*JX = JZ + 2*JXY
=> JX = M/20*a² + 3M/80*h² = M(a²/20 + 3h²/80)
1.5 LO(P/ℜ) = OG 
M*V(O/R) + IO(P).ωx
Est-ce que OG M*V(O/R) = 0 car V(O/R = 0.
IO(P) s'obtient avec le Théorème de Hyugens.
Est-ce que c'est un bon début ou ce n'est pas la peine de continuer ?
Bonjour,
Je m'étais assoupi. En fait je pensai avoir répondu.
Oui, à ta question. Oui, j'ai un facteur 2 qui a sauté dans la rédaction de ma réponse précédente.
Qu'obtiens tu pour Io?
Io = 1/2(Iox+Ioy+Ioz) = ...
Déjà je vous remercie de m'aider.
En fait, dans la formule du moment cinétique que j'ai donné, I représente une matrice d'inertie.
Re-,
Je suis ok avec ton raisonnement et ton résultat:
LO(P/ℜ) = OG M*V(O/R) + IO(P).ωx
le premier terme nul puisque
V(O/R = 0.
Et IO(P) lié à J par Th. de Huygens
J'essaierai tout même de trouver le temps de reformuler tout cela en utilisant Latex ... cela augmente la lisibilité.
Courage!
En appliquant le Théorème de Huygens :
(b²+c² -ab -ac)
IO(P) = IG(P) + M*(-ab a²+c² -bc)
(-ac -bc a²+b²)
Avec a,b et c les coordonnées du point G(0,0,h/4) et M la masse du solide P.
(a²+2h² 0 0)
IO(P) = M/20*(0 a²+2h² 0)
(0 0 2a²)
Ainsi :
LO(P/ℜ) = IO(P)*ωx
(a²+2h² 0 0) (w)
= M/20*(0 a²+2h² 0) * (0)
(0 0 2a²) (0)
((M/20*a²+2h²)ω)
= ( 0 )
( 0 )
Je pense que ça devrait être bon...
En tout cas je suis d'accord avec tes calculs ... avec juste une petite parenthèse mal tapropos dans la dernière expression
Bonjour,
Ce sujet date, mais je tente toutefois...
J'ai le même genre de calcul à faire, à savoir trouver le moment d'inertie d'une plaque an acier =7850kg/m3, de coté l=1.18m d'épaisseur e=0.035m.
J'ai utilisé la même méthode que celle décrite dans ce post par PerArGal, et j'arrive à l'expression du moment d'inertie : I = 1/6 x x I^4 x e
l'application numérique me donne un résultat complétement farfelu : 886
et d'un point de vue dimensionnel, ce résultat serait en kg.m²
Est-ce que quelqu'un pourrait m'aider ? Je ne trouve pas mon erreur...
Forcément, si apparait dans le calcul, j'aurais un souci de dimension...
Merci d'avance!
A bientot
Badab
Annuler
connectez vous