Niveau master

Moment dynamique

Posté par
Tauronamix 08-03-22 à 07:33

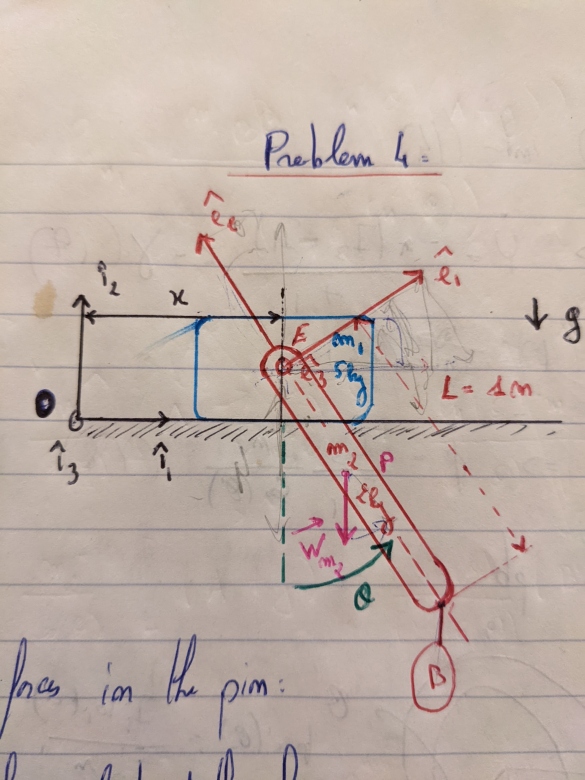
Bonjour, j'ai calculer le moment dynamique au point E du solide B par rapport au repère inertiel en dérivant le moment cinétique. Pour calculer le moment cinétique en un point quelconque du solide B j'ai utilisé cette définition:

$\vec{\sigma_{E/I}}=I_{E}.\omega _{B/I}\: +\:\vec{EG}\:\wedge\:\vec{V_{E/I}}$

Ensuite j'ai juste dérivé par rapport au repère inertiel et conserver toutes les composantes suivant mon vecteur e3. Voici ce que j'obtiens:

$\frac{2}{3}L\ddot{\theta}\:+\:\ddot{x}cos(\theta)-\dot{x}\dot{\theta}sin(\theta)=-sin(\theta)g$

Mon prof aux USA ne fait pas cette technique, il cacule le moment d'inertie en E en utilisant seulement I fois le vecteur rotation (donc la moitié de ce que j'ai fait). Mais ensuite dans il écrit ceci :

$\frac{d}{dt}({\vec{\sigma_{E}}})_{I}=\vec{M_{E}}+\vec{a_{E/I}}\:\wedge\:\vec{EG}m_{2}$

Avec M_E le moment en E généré par le poids et a l'accélération au point E du solide B and I. Le problème c'est qu'en utilisant sa technique on ne retombe pas sur le même résultat, alors ma question c'est pour quelle raison ?

Son résultat est similaire sauf qu'il n'a pas le terme en Xpoint Thetapoint sin(theta).

Merci d'avance pour votre aide.

Moment dynamique

Posté par re : Moment dynamique 08-03-22 à 13:33

Bonjour
Attention : dans le cas le plus général, le moment dynamique en un point A quelconque de l'espace n'est pas égal à la dérivée par rapport au temps du moment cinétique au même point A. Cela n'est vrai que dans un certains nombre de cas particuliers, cas particuliers tout de même très fréquents :
1° : le point A est confondu avec le point G ;
2° : le point A est fixe.
3° : A et G ont à chaque instant la même vitesse dans le repère d'étude.

Posté par re : Moment dynamique 08-03-22 à 16:11

Pour en revenir aux différents calculs. J'ignore l'objectif précis de cette étude et je ne connais pas exactement les notations de ton professeur. En supposant qu'il s'agisse d'établir l'équation différentielle vérifiée par . On peux appliquer au pendule de masse m2 le théorème du moment dynamique au point E en projection sur $\vec{e_3}$ dans le repère mobile lié au solide de masse m1. On est donc ramené à l'étude d'un simple pendule mobile autour de l'axe horizontal passant par E et perpendiculaire au plan de figure. Ce repère n'est pas galiléen : il est en translation rectiligne par rapport à un référentiel galiléen avec une accélération $\vec{a_{E/I}}$ . On peut donc faire l'étude comme s'il s'agissant d'un simple pendule soumis, à l'action de l'axe de rotation, à son poids et à la force d'inertie d'entraînement $-m_2\cdot\vec{a_{E/I}}$ .
Cela conduit à la relation vectorielle de ton professeur qui, une fois projetée sur $\vec{e_3}$ donne :
avec : $\overrightarrow{a_{E/I}}=a_{E/I}.\overrightarrow{i_{1}}$ ( $a_{E/I}$ pouvant être une valeur négative)

$I_{Ez}.\ddot{\theta}=-m_{2}.g.EG.\sin\left(\theta\right)-m_{2}.a_{E/I}.EG.\cos\left(\theta\right)$

$I_{Ez}$ : moment d'inertie de la tige de masse m₂ par rapport à son axe de rotation passant par E.
Sous toutes réserves...