Inscription / Connexion Nouveau Sujet
MOment dipolaire d'une molécule
Bonjour, je n'arrive pas à comprendre cet exercice, même avec la correction.
Voici l'énoncé et, j'ai mis la correction en PJ (elle comporte des schémas)
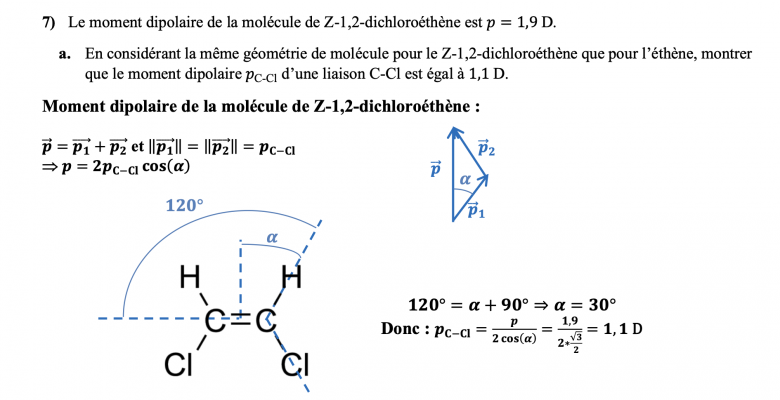
Le moment dipolaire de la molécule de Z-1,2-dichloroéthène est 𝑝 = 1,9 D.
a. En considérant la même géométrie de molécule pour le Z-1,2-dichloroéthène que pour l'éthène, montrer
que le moment dipolaire 𝑝C-Cl d'une liaison C-Cl est égal à 1,1 D."
J'ai plusieurs incompréhensions : Pourquoi la liaison C-H n'est pas prise en compte ?
Pourquoi pose on l'angle alpha ainsi ? Pourquoi ne pas prendre l'angle C-Cl ?
Pourquoi la formule est p = 2p(c-cl)cos(alpha) et pas 2p(c-cl)cos(alpha/2), comme c'est écris dans le cours ?
Merci d'avance pour votre aide
Bonjour
Les atomes H et C ont pratiquement même electronegativité. On les considère souvent pour simplifier les liaisons entre ces atomes comme non polarisées. Ensuite pour le calcul : on peut raisonner avec l'angle que l'on veut.
Bonjour,
Merci de votre réponse. Pour l'angle, si n'importe quel angle fonctionne alors pourquoi ne pas prendre celui de 120 ° que l'on connaît ?
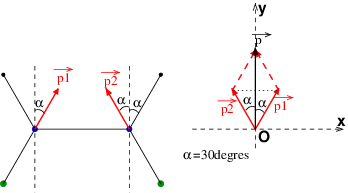
As-tu bien compris comment s'obtiennent les vecteurs moments dipolaires ? Chaque vecteur ou
possède la direction de l'axe de liaison Cl-C et est orienté de l'atome le plus électronégatif vers l'atome le moins électronégatif donc de Cl vers C. Pour plus de clarté, j'ai représenté ci-dessous ces vecteurs sur le "squelette" de la molécule. On voit bien que la détermination de la norme de
conduit à raisonner sur les côtés d'un losange donc à privilégier l'angle
 =30° de la figure. Il est cependant possible d'appliquer le théorème d'Al Kashi à un des triangles constituant ce losange en utilisant l'angle de 120° mais cela est moins immédiat.
=30° de la figure. Il est cependant possible d'appliquer le théorème d'Al Kashi à un des triangles constituant ce losange en utilisant l'angle de 120° mais cela est moins immédiat.
Il faut réfléchir dans les exercices au cas par cas et ne pas appliquer " à l'aveugle" des formules de cours démontrées dans un autre contexte.
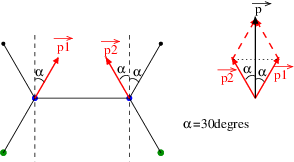
Si tu éprouves des difficultés sur les sommes de vecteurs, tu peux utiliser la méthode de projection des vecteur dans un repère (voir figure) comme tu le faisais dans le secondaire en mécanique. Les deux composantes du vecteur somme sont :
: la norme recherchée.
Encore une fois : ne pas utiliser à l'aveugle une formule de cours sans connaître précisément ses conditions d'applications et la signification des symboles utilisés.
Que représente l'angle  dans ton cours ? Peut-être l'angle entre les vecteurs
dans ton cours ? Peut-être l'angle entre les vecteurs et
.
Dans cet exercice,  désigne la moitié de cet angle...
désigne la moitié de cet angle...